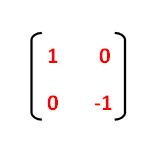
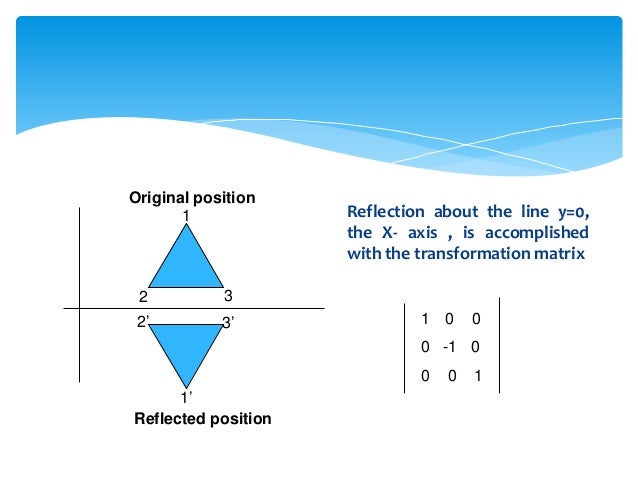
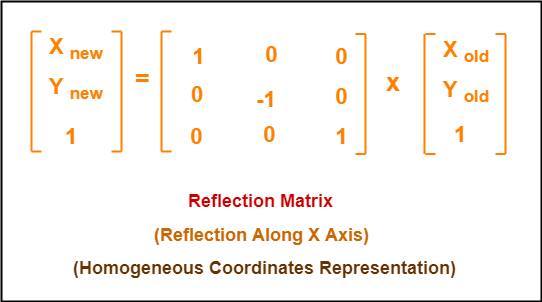
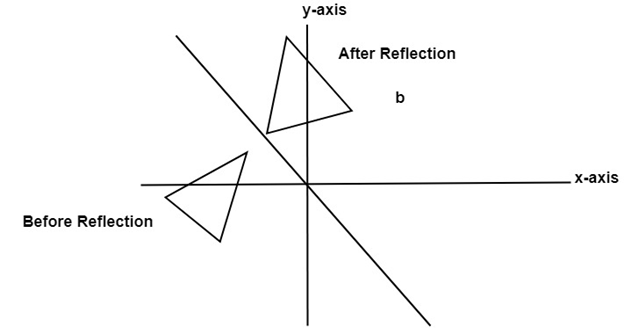
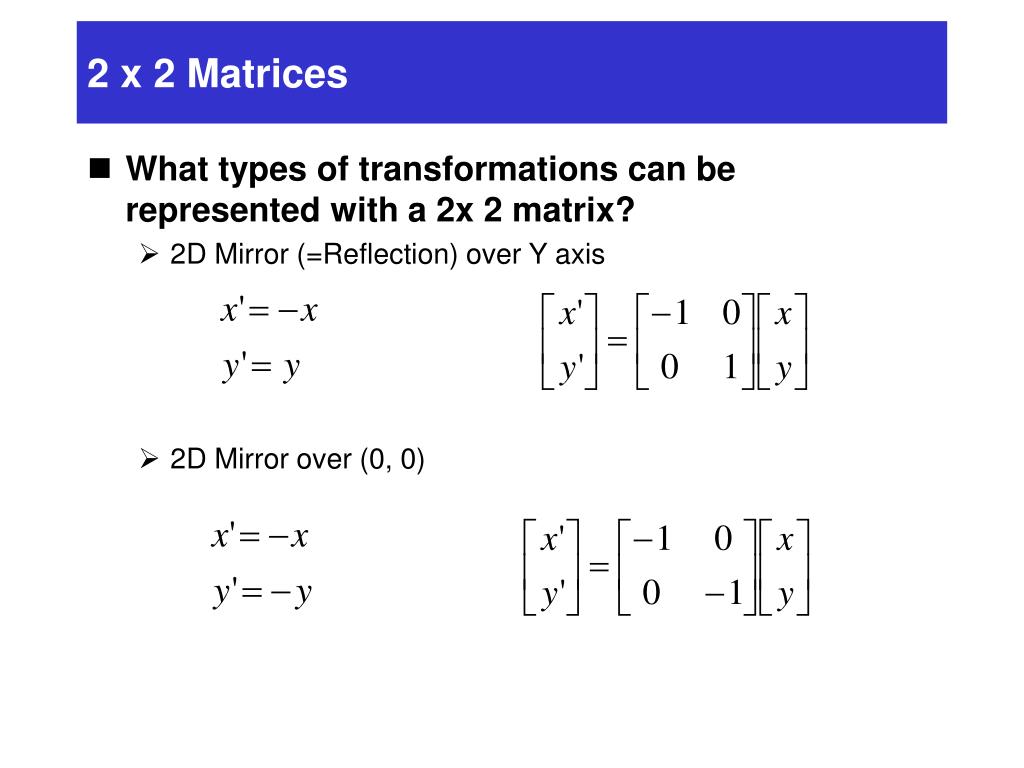
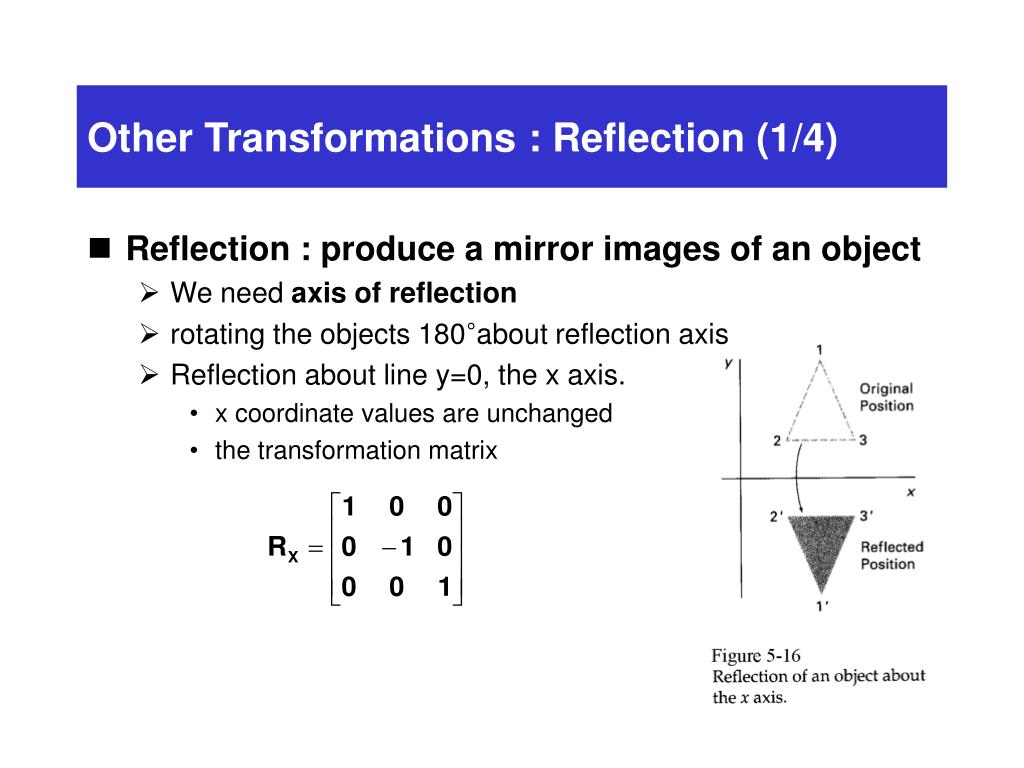
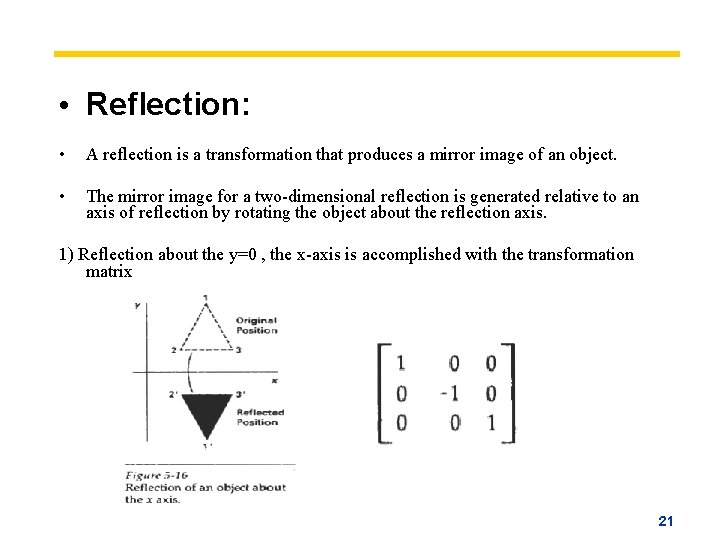
1 Reflection about xaxis The object can be reflected about xaxis with the help of the following matrix In this transformation value of x will remain same whereas the value of y will become negative Following figures shows the reflection of the object axis The object will lie another side of the xaxis 2 Let T R 2 → R 2 be a linear transformation of the 2 dimensional vector space R 2 (the x y plane) to itself which is the reflection across a line y = m x for some m ∈ R Then find the matrix representation of the linear transformation T with respect to the standard basis B = { e 1, e 2 } of R 2, where e 1 = 1 0, e 2 = 0 1 Reflect the point (5,4) in the line y = x;
Bestmaths
What is reflection in transformation
What is reflection in transformation- The vector law of reflection can be written in matrix form as k 2 = M k 1 Where the mirror matrix M is calculated to be M =I −2 ⋅n T M can be expanded as M 1 0 0 0 1 0 0 0 1 2 n x n y n z n x n y n z or M 1 2n x 2 2n xn y 2n x n z 2n xn y 1 2n y 2 2n yn z 2n x n z 2n yn z 1 2n z 2 After calculating this mirror matrix, any vector k1 Let Υ R 3 → R 3 be a reflection across the plane π − x y 2 z = 0 Find the matrix of this linear transformation using the standard basis vectors and the matrix which is diagonal Now first of, If I have this plane then for Υ ( x, y, z) = ( − x, y, 2 z) I get this when passing any vector, so the matrix using standard basis vectors is Y = ( − 1 0 0 0 1 0 0 0 − 2)



Matrices As Transformations
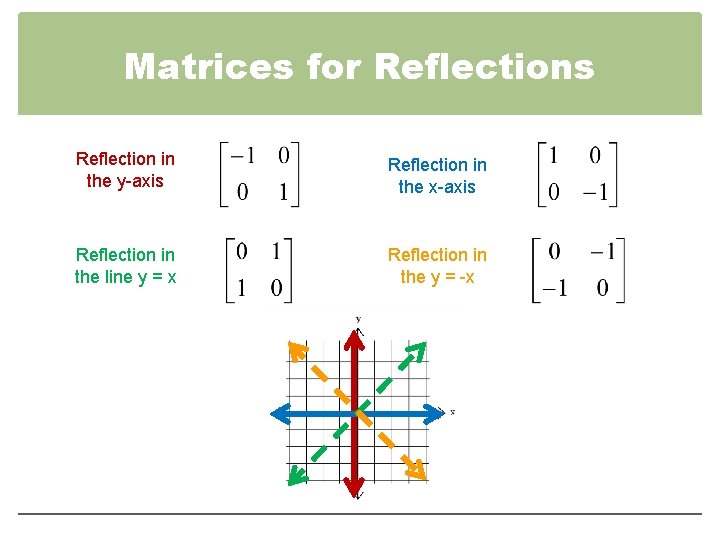
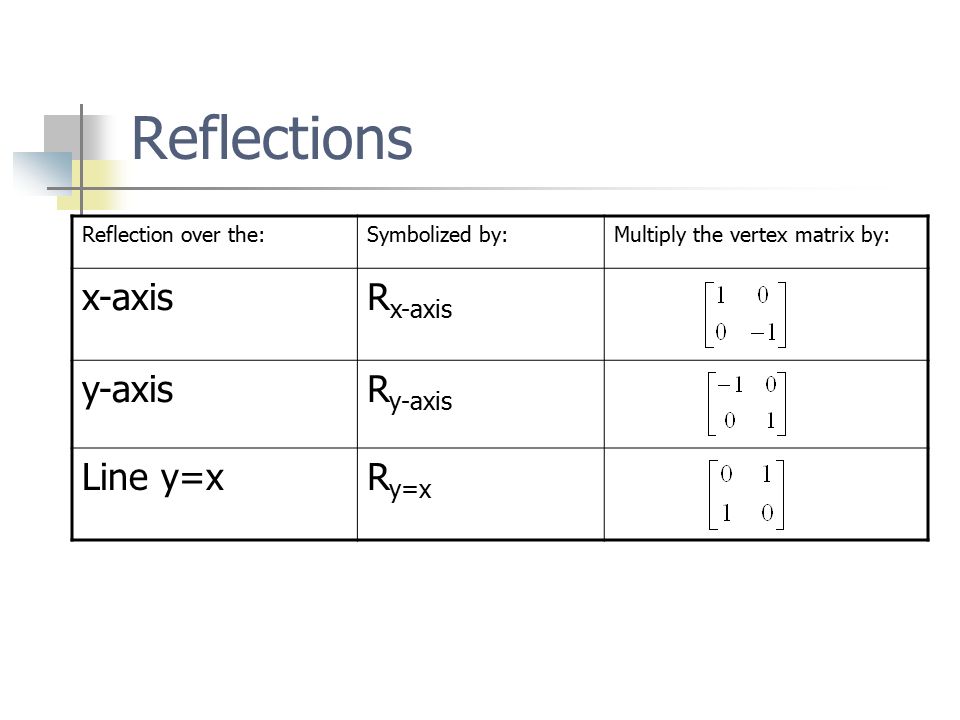
For a reflection over the x − axis y − axis line y = x Multiply the vertex on the left by 1 0 0 − 1 − 1 0 0 1 0 1 1 0To save time, the vertices of the unit square can be put into one 2 x 4 matrix eg Click here for another way of identifying transformation matrics Types of Transformation Matrices Reflections and Rotations The more common reflections in the axes and the rotations of a quarter turn, a half turn and a threequarter turn can all be represented by matrices with elements fromFind the image of the point (1,2) after a reflection in the line y = x followed by another reflection in the line y = x Find the equation of the line y = 3x 1 after being reflected in the line x y = 0 A Matrix Operator to Rotate any Point P( X, Y ) Through 90° 180°, 270° and 360° about the Origin
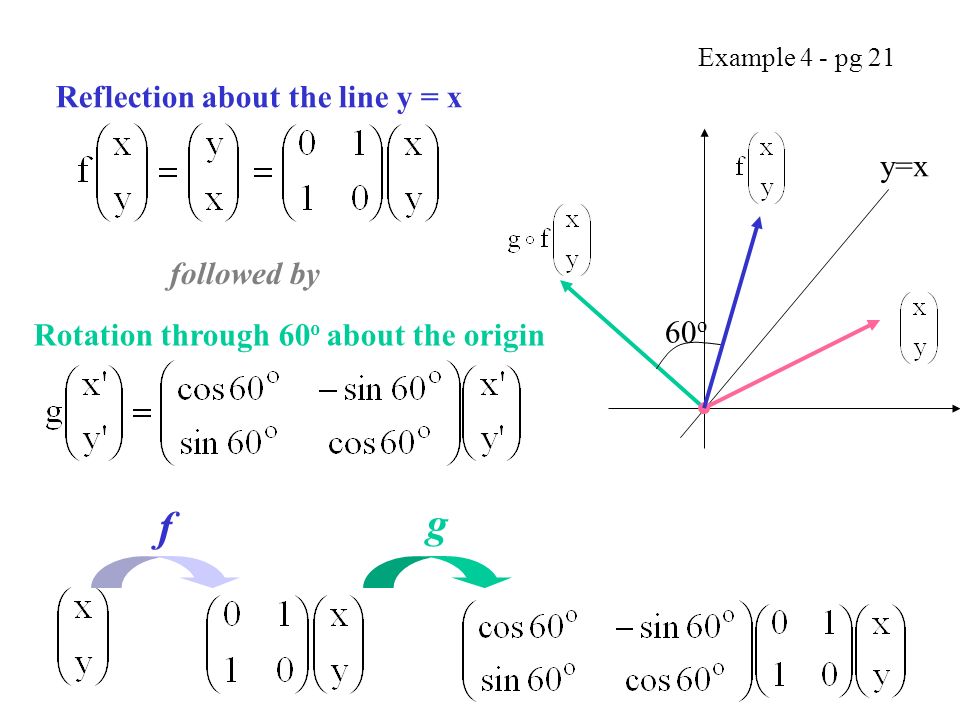
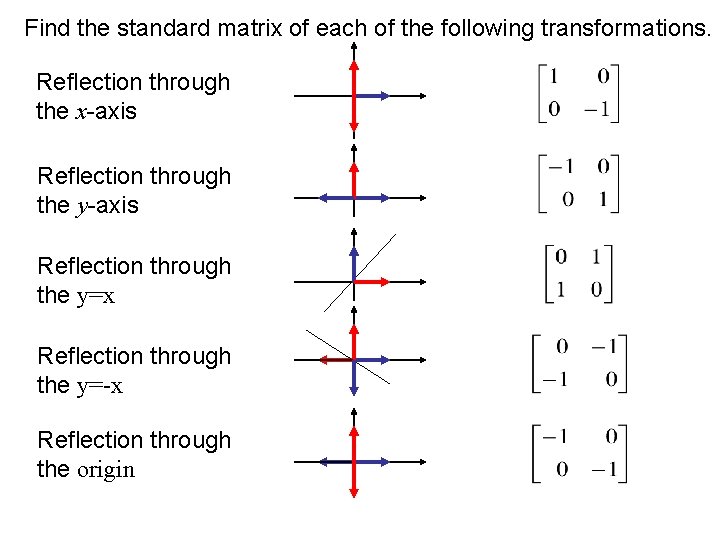
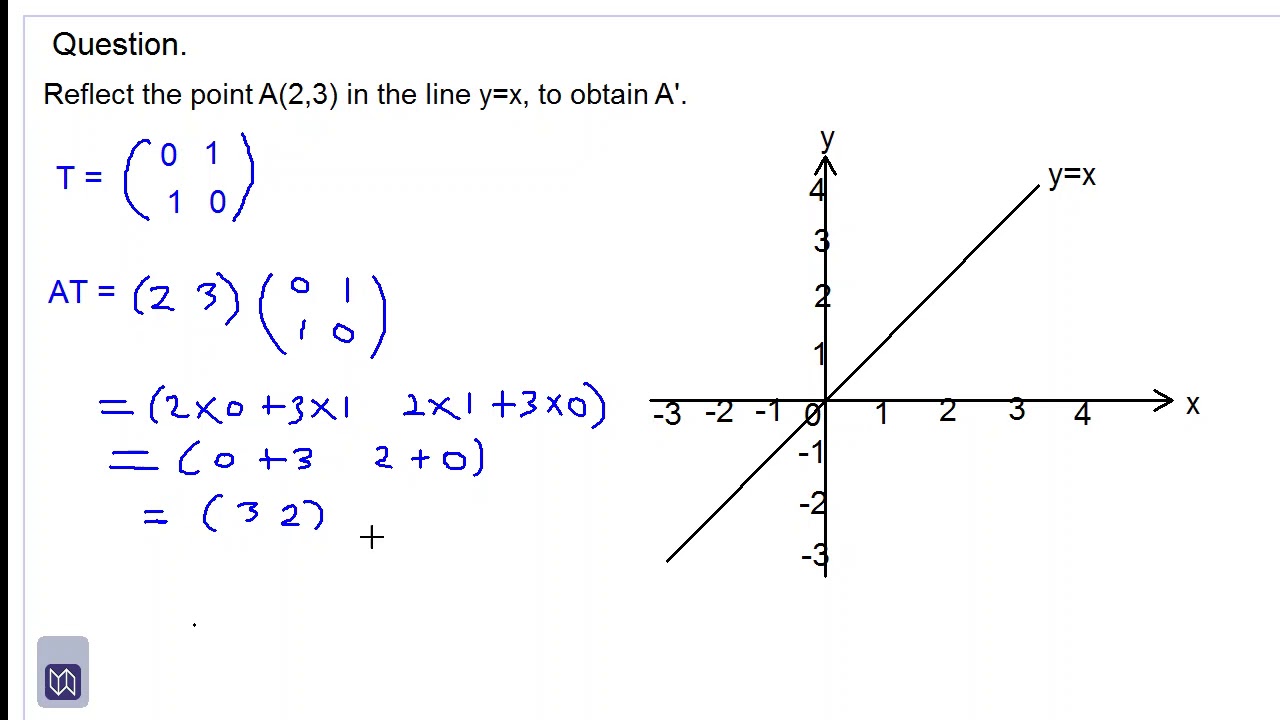
Hence, the matrix\(\begin{bmatrix}0&1\\1&0\\ \end{bmatrix}\) represents the reflection in the line y = x (c) Reflection in the line y = x Let R be the reflection in the line y = x, Then, R P(x, y)→ P'(y, x) If P'(x', y') is the image of P(x, y), then x' = y = 0x 1y y' = x = 1x 0y In the matrix form, this system can beOther transformations Besides basic transformations other transformations are reflection and shearing Reflection Reflection is a transformation that produces the mirror image of an object relative to an axis of reflection The mirror image is generated relative to an axis of reflection by rotating the object by 180 degree about the axisReflection about line y=x;
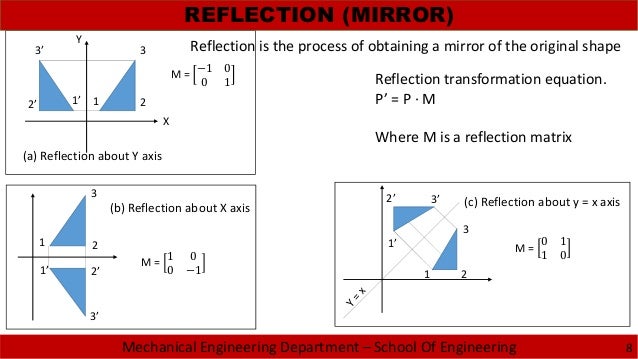
Y = x (x, y) → (y, x), and r y –x (x, y) → (–y, –x) It is easy to prove that the matrices for r x, r y = x, and r y = – x are as stated in the next theorem Matrices for r x, r y=x, and r y=–x Theorem 1 10 0 –1 is the matrix for r x 2 01 10 is the matrix for r y = x 3 0 –1 –1 0 is the matrix for r y = –x Proof of 1 10 0 –1 x y = 1 x 0 y22 Rotational transformation 11 y′ y z z′ x, x′ a Fig 22 Rotation around x axis axes of the rotated frame The upper left nine elements of the matrixH represent the 3×3 rotation matrix The elements of the rotation matrix are cosines of the angles between the axes given by the corresponding column and row Rot(x,α) = x y z ⎡ ⎢ ⎢ ⎣Step 1 First we have to write the vertices of the given triangle ABC in matrix form as given below Step 2 Since the triangle ABC is reflected about xaxis, to get the reflected image, we have to multiply the above matrix by the matrix given below Step 3 Now, let us multiply the two matrices Step 4




1 Point Match Each Linear Transformation With Its Chegg Com




Ejercicio De Transformation By Matrix
Answer is (D) (0, 1), (1, 0) After reflection in line x y = 0, y becomes x Therefore, we need a matrix which when multiplied by We observe that Hence, matrix of transformation is (0, 1), (1, 0) Please log in or register to add a comment Tutorial on transformation matrices in the case of a reflection on the line y=xYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXAMSOLUTIONS WEBSITSo rotation definitely is a linear transformation, at least the way I've shown you Now let's actually construct a mathematical definition for it Let's actually construct a matrix that will perform the transformation So I'm saying that my rotation transformation from R2 to R2 of some vector x can be defined as some 2 by 2 matrix




Linear Transformation Combination Of Ccw 90 Rotation And Reflection On Y X With Product Of Matrix Youtube




13 Find The Matrix Which Represents The Combined Transformation Of A Reflection In The X Axis Followee By A Reflection In The Line Y X
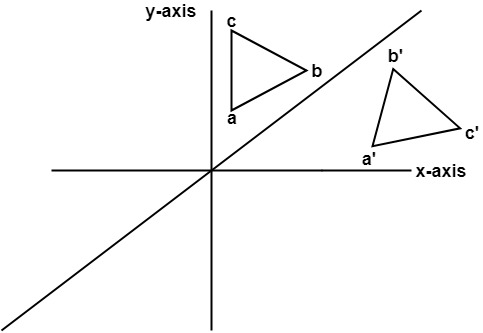
The resulting orientation of the two figures are oppositeThe linear transformation rule (p, s) → (r, s) for reflecting a figure over the oblique line y = mx b where r and s are functions of p, q, b, and θ = Tan 1 (m) is shown below Finding the linear transformation rule given the equation of the line of reflection equation y = mx b involves using a calculator to find angle θ = Tan 1 (mThe linear transformation matrix for a reflection across the line $y = mx$ is $$\frac{1}{1 m^2}\begin{pmatrix}1m^2&2m\\2m&m^21\end{pmatrix} $$ My professor gave us the formula above with no explanation why it works I am completely new to linear algebra so I have absolutely no idea how to go about deriving the formula




Matrices As Transformations



Matrix Corresponding To Rotation Matrix Corresponding To Reflection Rotation And Reflection Y Tan X Ppt Download
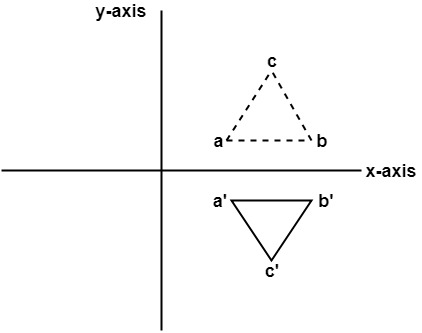
3D Reflection in Computer Graphics Reflection is a kind of rotation where the angle of rotation is 180 degree The reflected object is always formed on the other side of mirror The size of reflected object is same as the size of original object Consider a point object O has to be reflected in aReflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)Mirror transformation matrix Extended Keyboard;



An Important Linear Transformation In Calculus Is The Chegg Com



Reflection Transformation Matrix
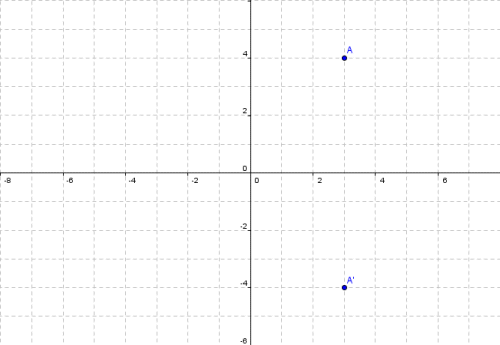
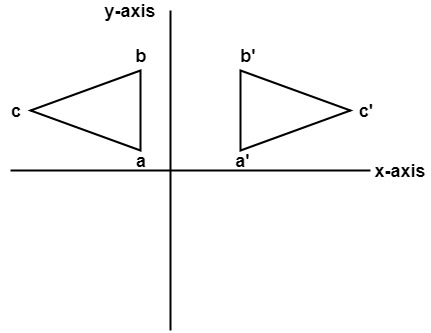
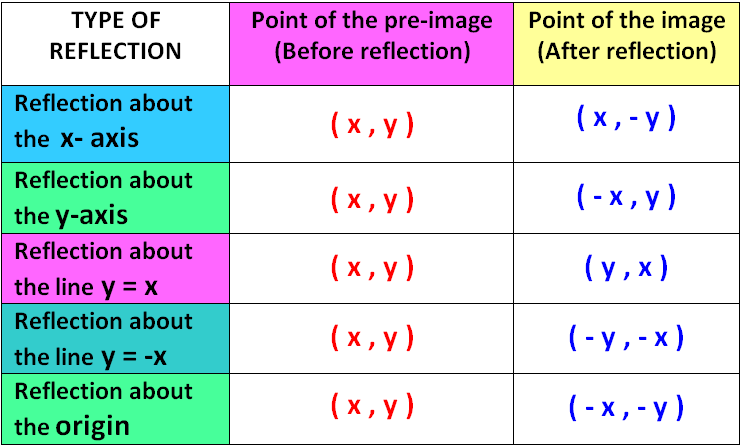
Let P(x, y) be any point in the 2D coordinates plane The reflection of this point P(x, y) in x axis is clearly the point P'(x, y) Similarly the reflection of the P' in the line y = x is the point P''(y, x) Point P" can also be obtainedIf (a, b) is reflected on the line y = x, its image is the point (b, a) Geometry Reflection A reflection is an isometry, which means the original and image are congruent, that can be described as a "flip" To perform a geometry reflection, a line of reflection is needed;Transformations and Matrices A matrix can do geometric transformations!



1



Matrices As Transformations
As an example, consider the line y = 2x, and a point A with xy coordinates x = 6, y = 3 Point A, with xy coordinates of ( 6, 3) is to be reflected in the line y = 2x There is a general form for a matrix corresponding to a reflection in the line y = (tan θ ) x, where θ is the angle between the xHave a play with this 2D transformation app Matrices can also transform from 3D to 2D (very useful for computer graphics), do 3D transformations and much much more The Mathematics For each x,y point that makes up the shape we do this matrix multiplicationReflection The second transformation is reflection which is similar to mirroring images Consider reflecting every point about the 45 degree line y = x Consider any point Its reflection about the line y = x is given by , ie, the transformation matrix must satisfy which implies that a = 0, b = 1, c = 1, d = 0, ie, the transformation matrix that describes reflection about the line y = x




Define The Terms With Example 1 Reflection 2 Shearing




Effect Of Applying Various 2d Affine Transformation Matrices On A Unit Square Note That The Reflection Matrices Are Matrices Math Studying Math Math Formulas
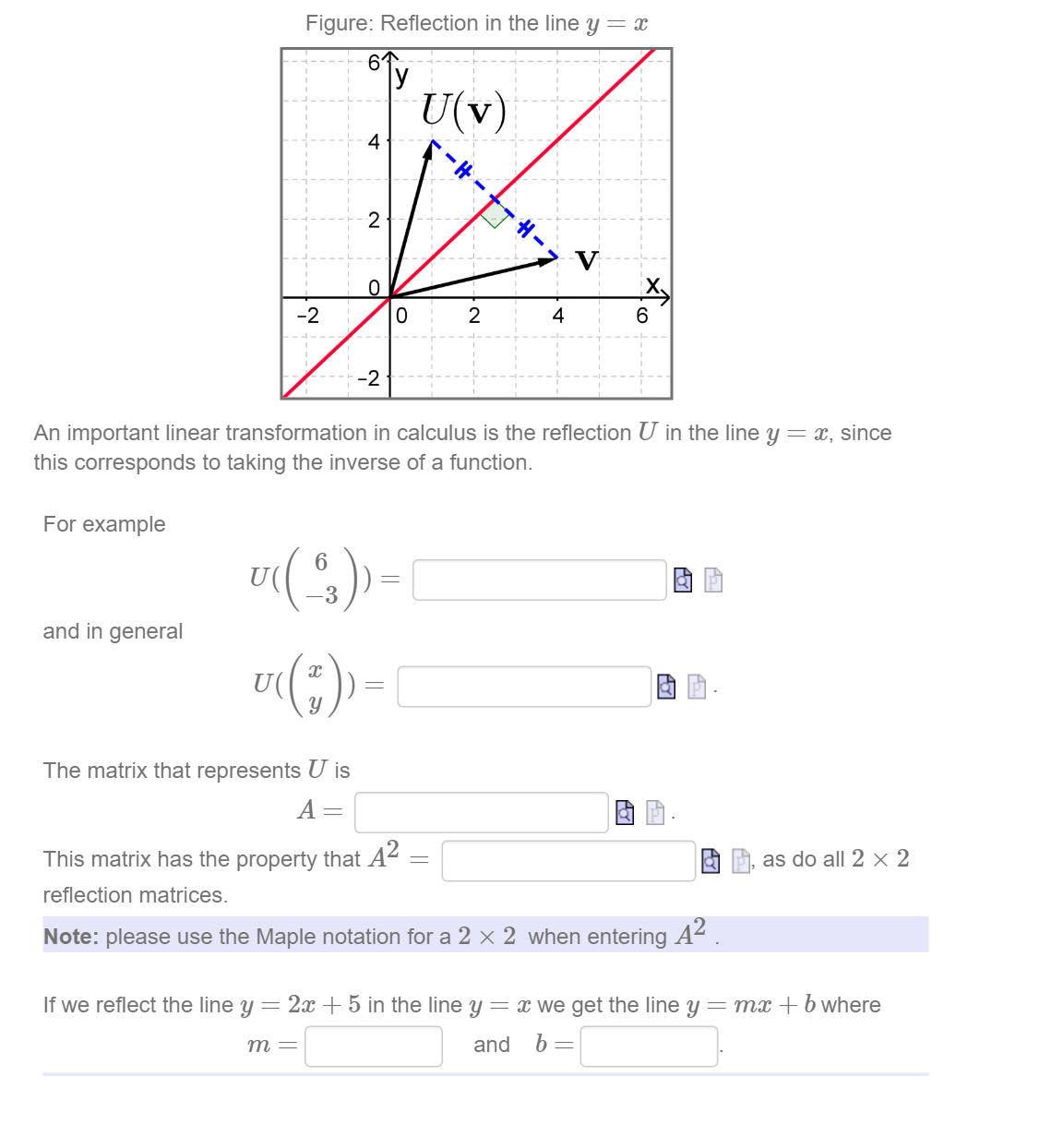
Reflection Transformations in 2Space Let such that and suppose that we want to reflect across the axis as illustrated Thus the coordinate of our vector will be the opposite to that of our image The following equations summarize our image Thus our standard matrix is , and in form we get that Of course there are other types of reflection Let T R 2 →R 2, be the matrix operator for reflection across the line L y = x a Find the standard matrix T by finding T(e1) and T(e2) b Find a nonzero vector x such that T(x) = x c Find a vector in the domain of T for which T(x,y) = (3,5) Homework Equations The Attempt at a Solution a I found T = 0 11 0Computational Inputs » line of reflection Compute Input interpretation Reflection matrix Transformation Matrix form Visual representation Download Page POWERED BY THE WOLFRAM LANGUAGE Related Queries rotate (1,2) by 45 degrees anticlockwise;




Reflection Transformation Matrix




Chapter 4 Chapter Content 1 Real Vector Spaces
Hence the transformation U represented by matrix P is a reflection in the line y = x It may be easier to sketch this so you can visualise the transformation ⇒ All question b is telling us is if we multiply matrix P by \( \left(\begin{array}{c}a\\ b\end{array}\right) \) we will get the coordinates \( \left(\begin{array}{c}3 2a\\ b 1\endReflectionMatrixv gives the matrix that represents reflection of points in a mirror normal to the vector vDerive the matrix in 2D for Reflection of an object about a line y=mxc written 25 years ago by profvaibhavbadbe ♦ 780 modified 14 months ago by sanketshingote ♦ 570 2d transformation matrix



4 4 Geometric Transformations With Matrices Objectives To



2 1 Fundamental Of Computer Graphics
More Matrix Transformations Fill in the matrices for the following transformations Transformation Matrix Transformation Matrix A Reflection in the x axis ⎛⎞ ⎜⎟ ⎝⎠ N Rotation by 45°clockwise about the origin ⎛⎞ ⎜⎟ ⎝⎠ B Rotation by 30°clockwise about the origin ⎛⎞ ⎜⎟ ⎝⎠ O Reflection in the y axisConflict between reflection matrix and rotation matrix Consider the following matrix used for reflection This matrix produces the reflection across y=x according to B = T× A where T is the above Transformation Matrix Things are clear till now Then I was introduced to rotation and taught that every reflection is some sort of rotationTherefore the matrix of the transformation is I2 Thus we have derived the matrix for a reflection about a line of slope m Alternatively, we could have also substituted u x = 1 and u y = m in matrix (2) to arrive at the same result Topology of reflection matrices
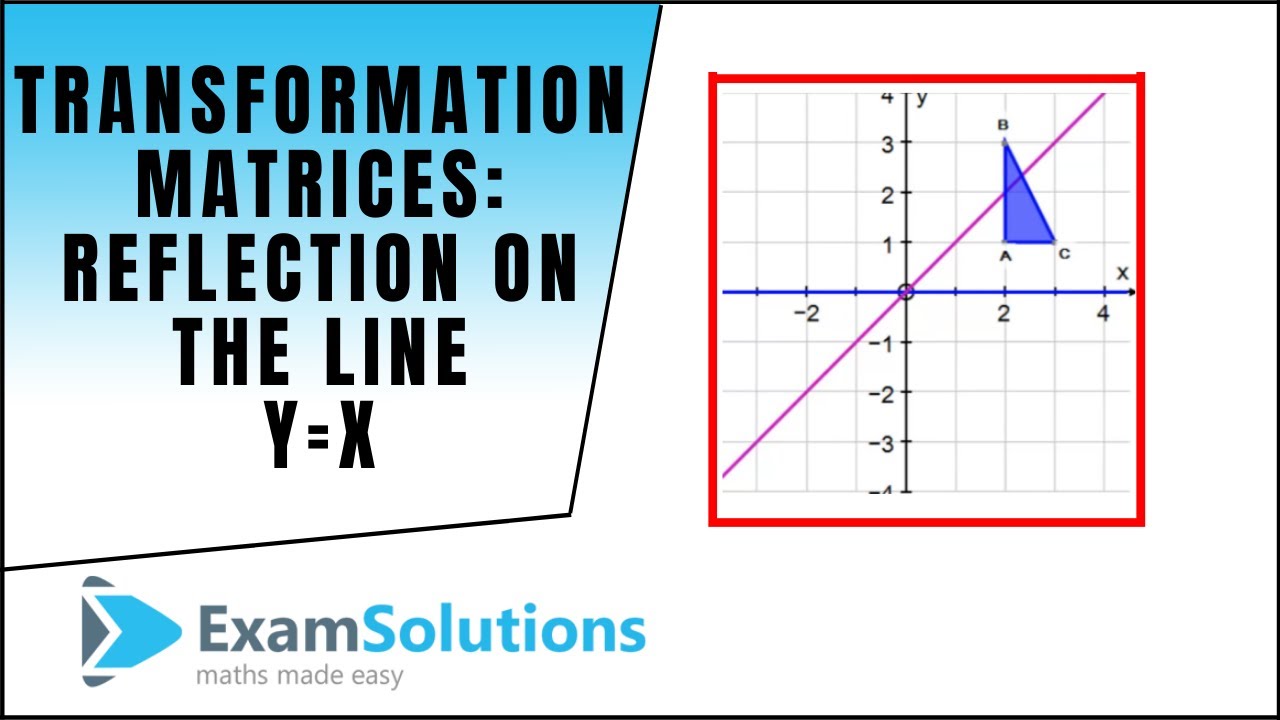



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube



Reflection In 2 D
Matrix Transformation Examples, solutions, videos, and lessons to help High School students learn to work with 2 × 2 matrices as a transformations of the plane, and interpret the absolute value of the determinant in terms of area Common Core HSNVMC12A reflection about y = x represented by a matrix and an affine transform A reflection about the lines y = x can also be represented both ways, as a matrix multiplication and an affine transformation The transformation matrix usually has a special name such as dilation, contraction, orthogonal projection, reflection, or rotation Transformation Matrices Dilation and Contraction We give several examples of linear transformations from $\mathbb{R}^2$ to $\mathbb{R}^2$ that are commonly used in plane geometry




Transformation Reflection Over The Line Y X Youtube




In This Problem We Are Dealing With Transformations Chegg Com
Transformation 1 Refection in the xaxis The image of (1, 0) is (1, 0) The image of (0, 1) is (0, 1) So the matrix is Transformation 2 Enlargement sf 2 centre (0, 0) This matrix is Combined transformation Since we wish to reflect first then enlarge, the correct order to multiply the matrices is =X ′ = x k y {\displaystyle x'=xky} and y ′ = y {\displaystyle y'=y} Written in matrix form, this becomes x ′ y ′ = 1 k 0 1 x y {\displaystyle {\begin {bmatrix}x'\\y'\end {bmatrix}}= {\begin {bmatrix}1&k\\0&1\end {bmatrix}} {\begin {bmatrix}x\\y\end {bmatrix}}} AY x 8 For following transformations, T Rd 4 Re, state what the transformation T represents and determine the image of the equation f(x) x 0 0 2 EXERCISE Transformations with matrices 1 Identify the dilations and/or œflections descñbed by the following matrices Find the image of the point (3, 5) under the above transformations in question 1



Content Linear Transformations And Matrices



Bestmaths
Introduction We learned in the previous section, Matrices and Linear Equations how we can write – and solve – systems of linear equations using matrix multiplication On this page, we learn how transformations of geometric shapes, (like reflection, rotation, scaling, skewing and translation) can be achieved using matrix multiplicationThis is an important concept used inQuestion (b) The transformation k is the reflection in the line y = x 7 By using the translation h that maps the point (0,7) to the origin, and its inverse h1, find the affine transformation k in the form k(x) Bxb, where B is a 2 x 2 matrix and b is a column vector with two components 5Transformation matrix = ( 0 − 1 1 0) b Translation Translation is a term used in geometry to describe a function that moves an object a certain distance The object is not altered in any other way It is not rotated, reflected or resized In a translation, every point of the object must be moved in the same direction and for the same distance



2d Reflection In Computer Graphics Definition Examples Gate Vidyalay




Reflection Transformation Matrix
Usually you should just use these two rules T (x)T (y) = T (xy) cT (x) = T (cx) Where T is your transformation (in this case, the scaling matrix), x and y are two abstract column vectors, and c D (y,x) ANSWER A If we take mirror reflection of a points(x,y) along the line Y=X then the point becomes_____ A (x,y) B (y,x) C (x,y) D (y,x) ANSWER D The number of matrices required to rotate an object about a point(1,1) are_____ A 1 B 2 C 3 D 4 ANSWER C In Xshear transformation point(x,y)becomes_____ A (xyb,xay) B (xyb,y)In this lesson we talked about how to reflect a point in the line y=x




Transformations With Matrices Easing The Hurry Syndrome



Computer Graphics Reflection Javatpoint




1 Point Match Each Linear Transformation With Its Chegg Com




Reflection Transformation Matrix




9 Matrices And Transformations Pdf Free Download



Computer Graphics Reflection Transformation Student Study Hub




Fp1 Matrices Transformations Ppt Download



Reflection Transformation
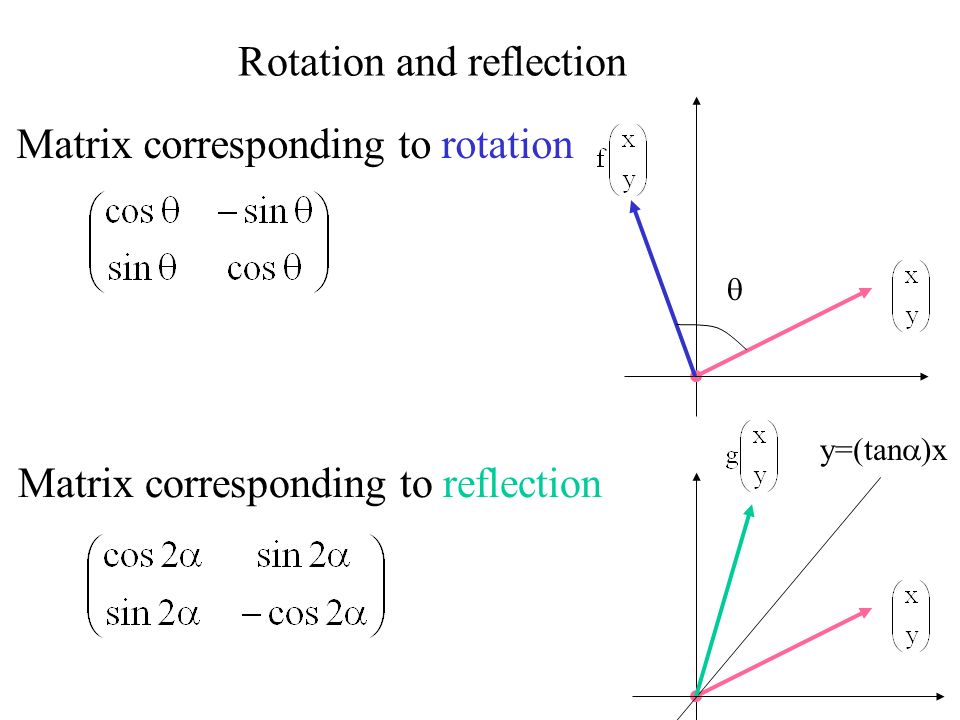



Matrix Corresponding To Rotation Matrix Corresponding To Reflection Rotation And Reflection Y Tan X Ppt Download




Reflection Transformation
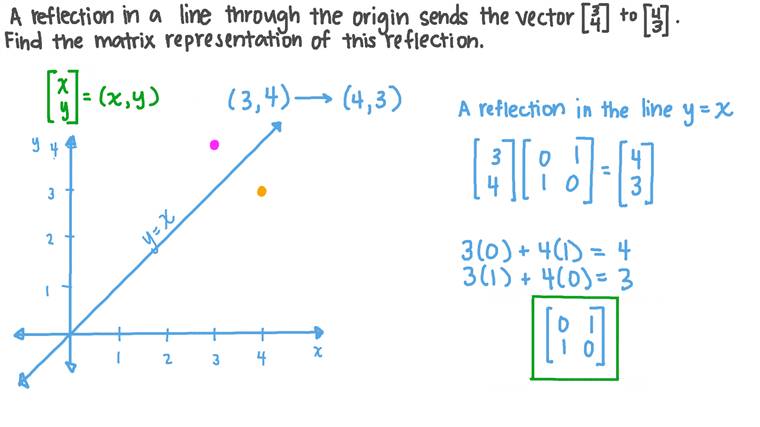



Lesson Linear Transformations In Planes Reflection Nagwa




The Matrix Of The Transformation Reflection In The Line X Y 0 Is
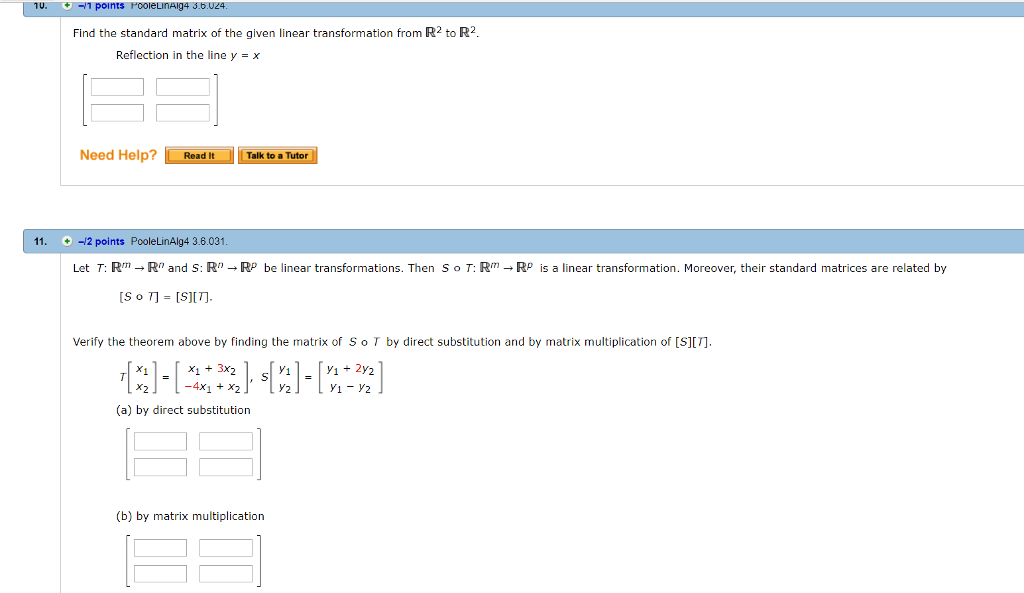



Find The Standard Matrix Of The Given Linear Chegg Com




Match Each Linear Transformation With Its Matrix Chegg Com
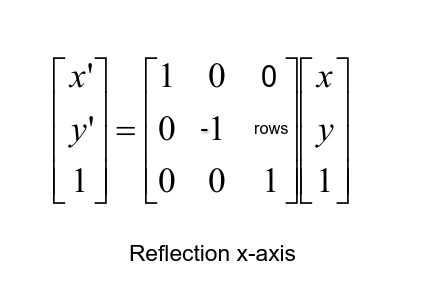



Image Transformations Using Opencv In Python Python Code




Matrix Corresponding To Rotation Matrix Corresponding To Reflection Rotation And Reflection Y Tan X Ppt Download




3d Reflection In Computer Graphics Definition Examples Gate Vidyalay




Linear Transformation From R 2 To R 2 Given In Figure Problems In Mathematics




2d Reflection In Computer Graphics Tutorial And Example




Matrix Representation Of 2d Transformation Javatpoint




The Matrix For The Linear Transformation Of The Reflection Across A Line In The Plane Problems In Mathematics




Computer Graphic Transformations In 2d




Match Each Linear Transformation With Its Matrix A Chegg Com




Do You Know Matrix Transformations
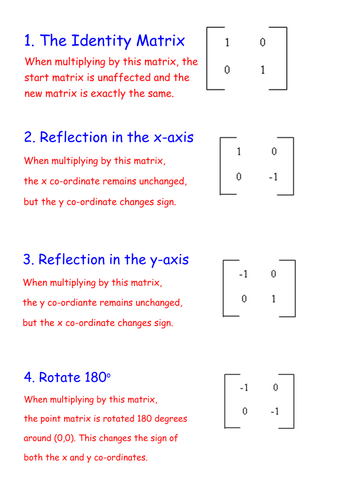



The 8 Matrix Transformations Teaching Resources




Linear Transformations With Matrices Lesson 10 Reflection In The Line Y X Youtube




The Matrix Of The Transformation Reflection In The Line X Y 0 Is
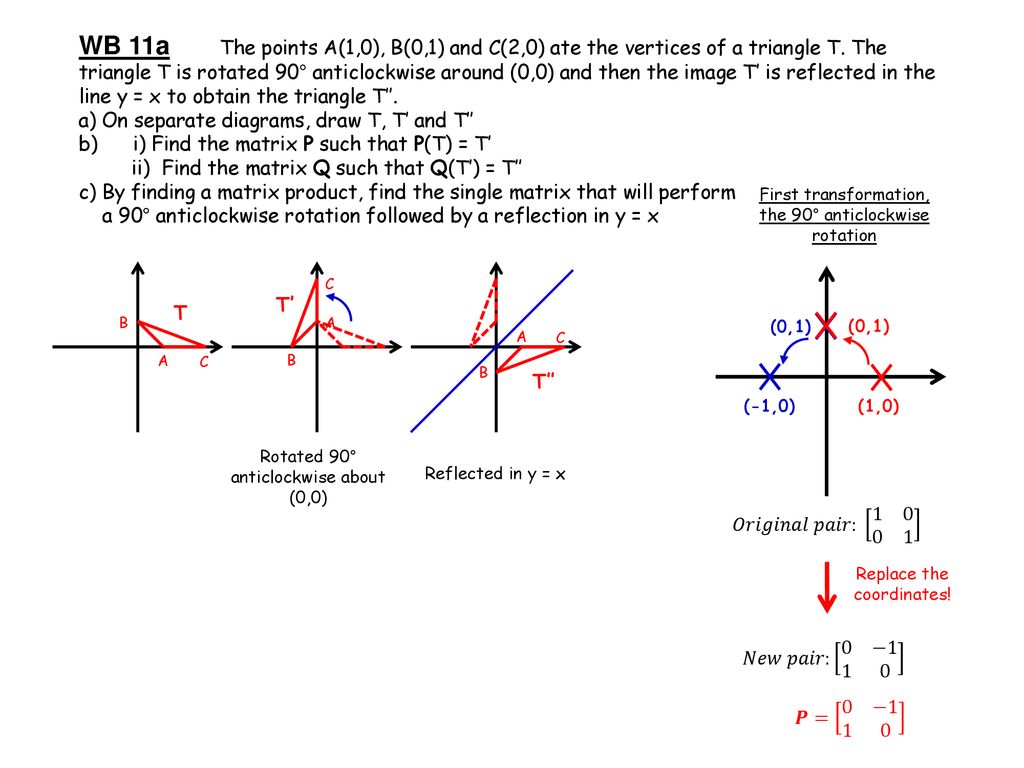



Fp1 Matrices Transformations Ppt Download



Reflection Transformation Solutions Examples Videos
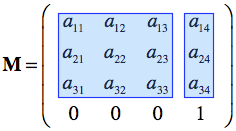



Spatial Transformation Matrices




Matrix Transformations Advanced Higher Maths




3d Transformation



Computer Graphics Reflection Javatpoint



2 4 Modeling Motion With Matrices Pre Calc A Vocabulary Transformations Translation Reflection Rotations Dilations Ppt Download




Consider The Following Transformation Reflection In Chegg Com



Transformation Of Graphs Using Matrices Reflection




Reflection Rules How To W 25 Step By Step Examples




Reflection Transformation Matrix



1




Reflection Rules How To W 25 Step By Step Examples




Reflection Rules How To W 25 Step By Step Examples
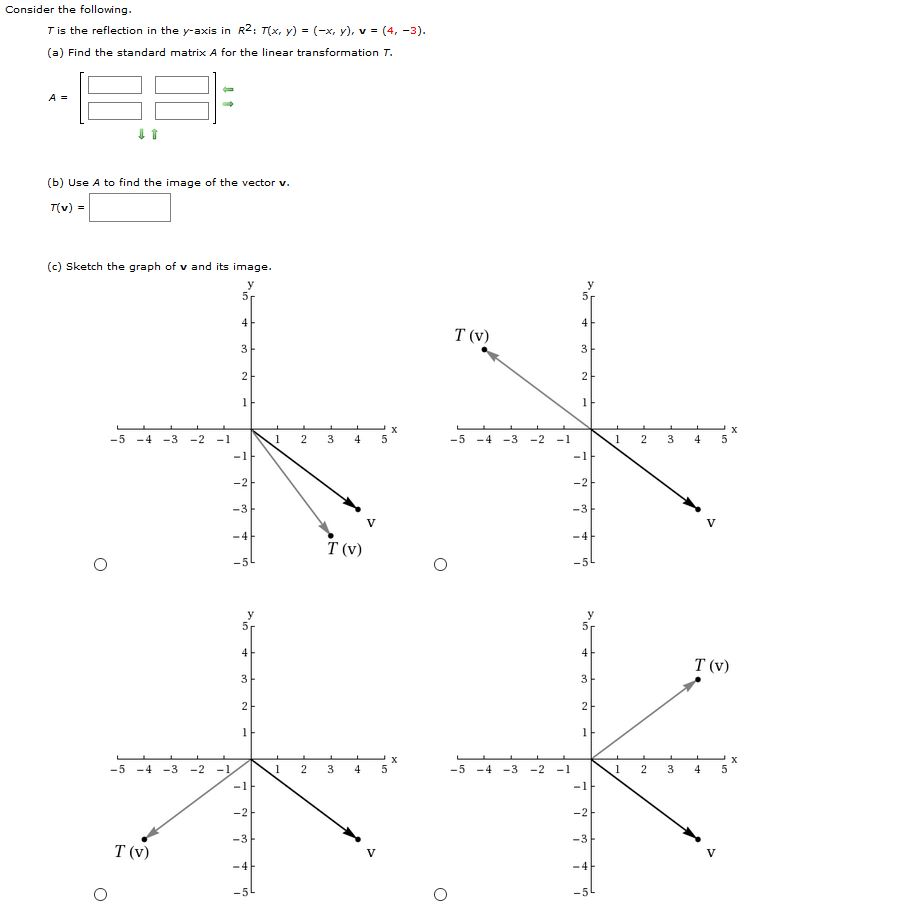



Consider The Following T Is The Reflection In The Chegg Com
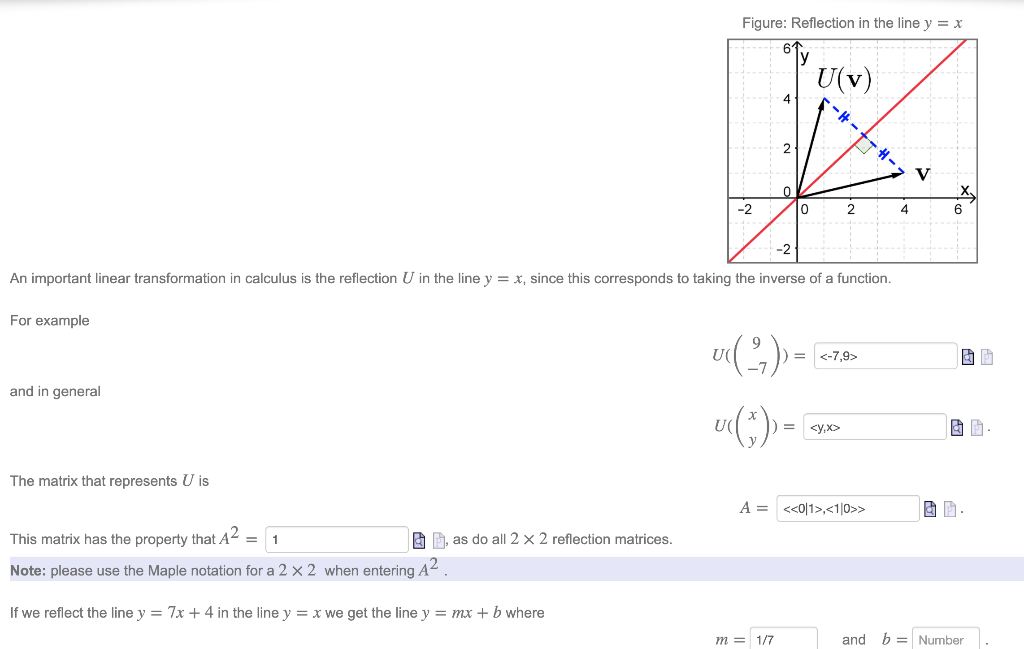



Figure Reflection In The Line Y X 61 U V 4 2 Chegg Com




Matrix Reflections Youtube
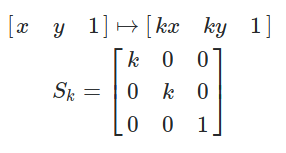



Understanding 3d Matrix Transforms By Shukant Pal The Startup Medium



Matrices As Transformations



Mafiadoc Com Download 01 Linear Transformations 59f8de9e1723dda34d77e4df Html




Reflection In The Line Y X Transformation Matrix Youtube
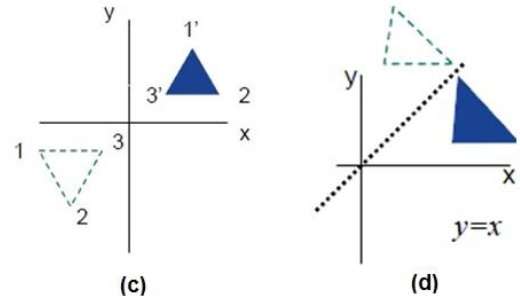



2d Transformation Tutorialspoint




Transformations Describing Reflections Doodlelearning




Graphics 2 D Geometric Transformations Cgvr Korea Ac



Ppt Modeling Transformation Powerpoint Presentation Free Download Id



Computer Graphics Reflection Javatpoint



Ppt Two Dimensional Geometric Transformations Ch5 참조 Powerpoint Presentation Id



1 9 The Matrix Of A Linear Transformation




The Matrix Of The Transformation Reflection In The Line X Y 0 Is




Reflection Transformation Matrix




What Is A Linear Transformation Quora




Helps For Making A Computer Animated Video Reflection Matrices Here




2d Transformation Important Notes For 2nd Year Bscit Sem 4 Visicomp Codder
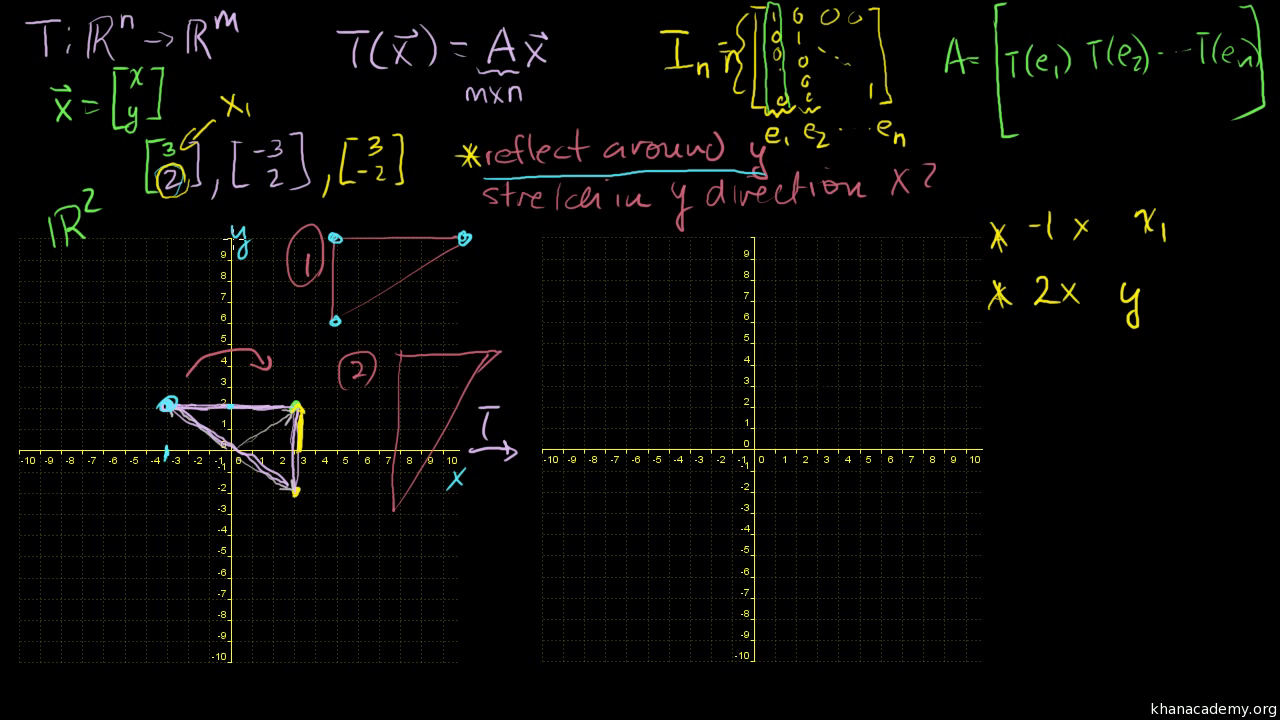



Linear Transformation Examples Scaling And Reflections Video Khan Academy




The Line X 0 Novocom Top
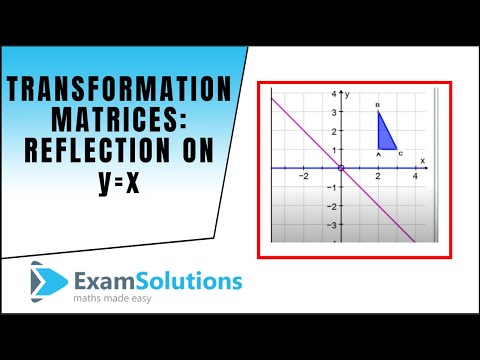



Linear Transformations Reflections Examsolutions



1
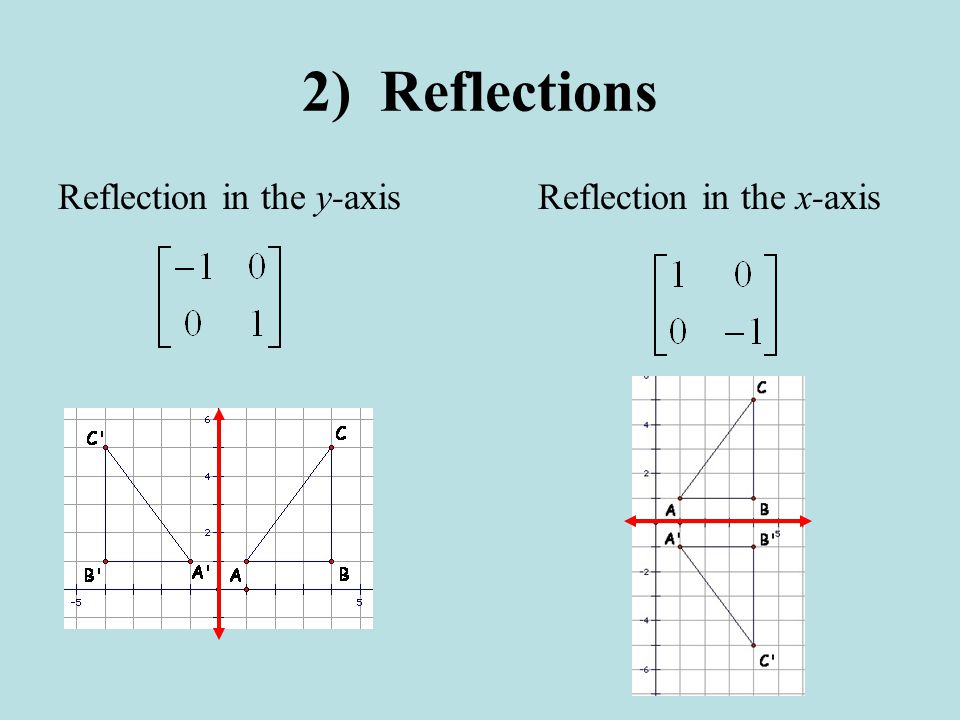



4 4 Transformations With Matrices Ppt Video Online Download




Give 3d Transformation Matrix For 1 Translation 2 Scaling 3 Rotation 4 Reflection 5 Shear
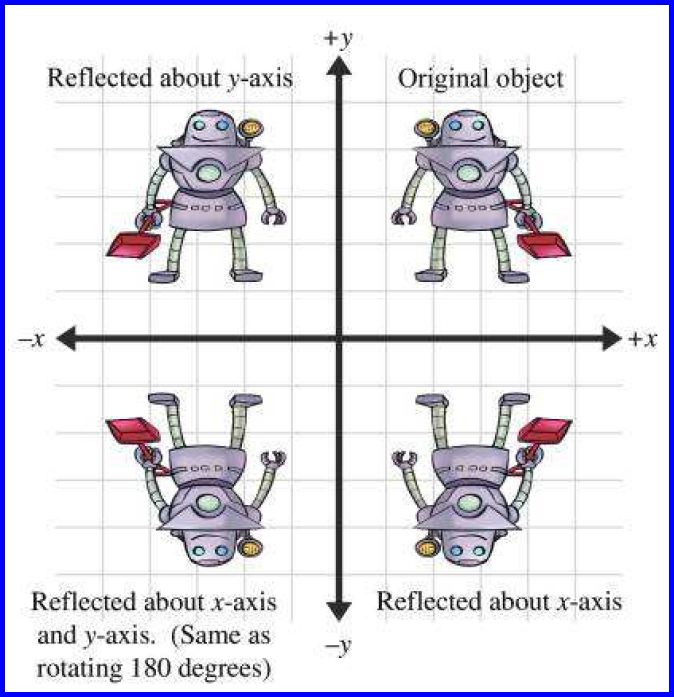



Matrices In Computer Graphics Dalao S World




Line Of Reflection Y 0 Novocom Top
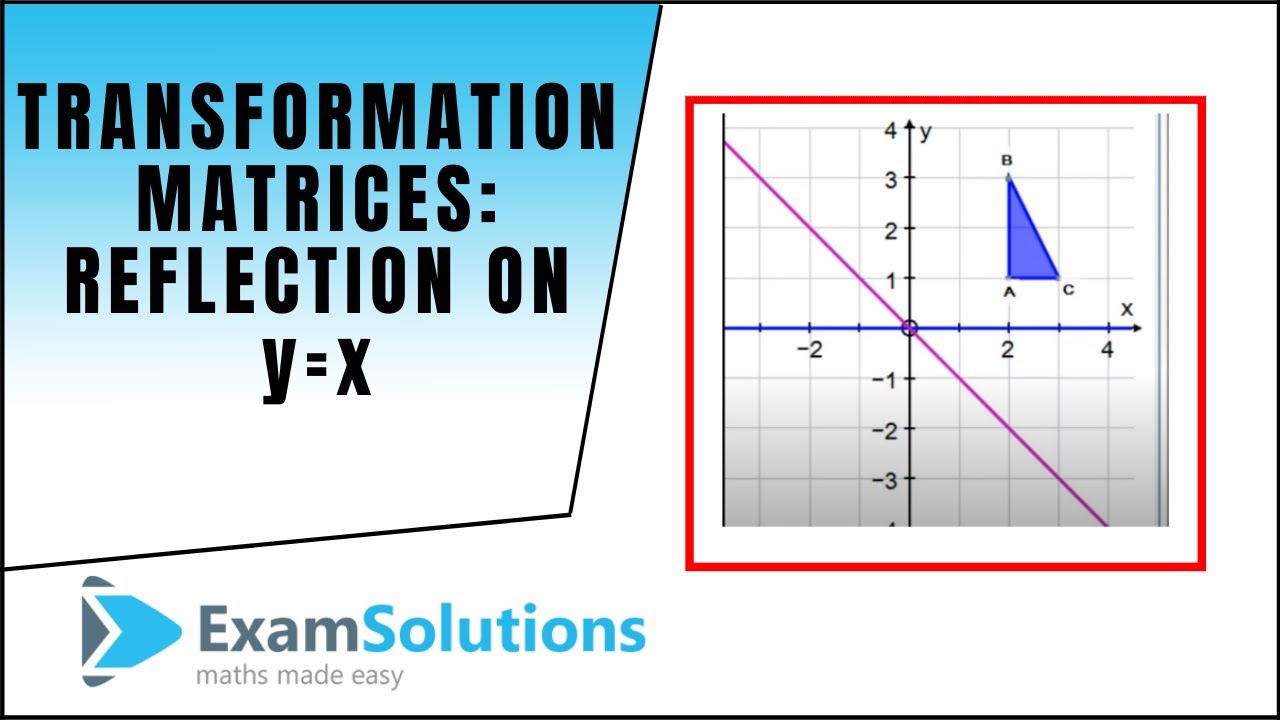



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube
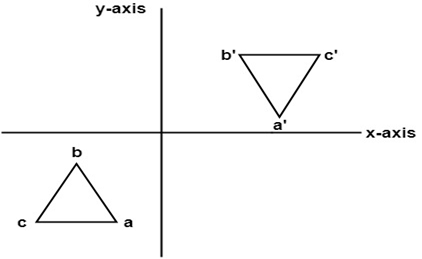



Computer Graphics Reflection Javatpoint




Do You Know Matrix Transformations




Match Each Linear Transformation With Its Matrix A Chegg Com



1



2d Shearing In Computer Graphics Definition Examples Gate Vidyalay



Line And Character Attributes 2 D Transformation 1



Computer Graphics Reflection Javatpoint



Math Alive Geometry 1




Transformation Using Matrices Geometry Transformations Mathplanet



Transformation Matrix For Reflection In Y X Youtube



Http Web Yonsei Ac Kr Hgjung Lectures Mat3 06 linear transformations Pdf



0 件のコメント:
コメントを投稿