If y=e(1/2)log(1tan2 x), then (dy/dx) is equal to (A) (1/2)sec2x (B) sec2x secx tanx (D) e(1/2)log(1tan2 x) Check Answer and Solution for aboveTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `Solve x dy/dxy=y^2logx`Given that dy/dx=log10 (xy), y(0)=1, find y(02) using modified Euler's method MATHEMATICS3 question answer collection
If Y X 2 1 Log X X 2 1 Prove That X 2 1 Dy Dx Xy 1 Quora
If y=log(1-x^2/1 x^2) find dy/dx
If y=log(1-x^2/1 x^2) find dy/dx- Share with your friends Share 3 Follow 8 Manbar Singh, Meritnation Expert added an answer, on Manbar Singh answered this We have, y = log x cos x x 2 1 x 2 1 Let y = u v where u = log x cos x and v = x 2 1 x 2 1 Now, y = u v ⇒ dy dx = du dx dv dx 1 Let u = log x cos x ⇒ log u = cos x log log x ⇒ 1 u Find dy/dx (x) 1/2 (y) 1/2 = (a) 1/2 Mention each and every step Queries asked on Sunday & after 7pm from Monday to Saturday will be answered after 12pm the next working day Kindly Sign up for a personalised experience




Mathematics Statistics 1 Pages 101 150 Flip Pdf Download Fliphtml5
Stack Exchange network consists of 179 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeSee the answer See the answer done loading Use logarithmic differentiation to find dy/dx y= (x1) (x2)/ (x1) (x2) The answer is dy/dx= 2 (x^22)/ (x1)^2 (x2)^2 I just need to see stepbystep how to solve Thank you!Solution for dy dx?
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(1x^2)dy/dx=1y^2`If y = sec –1 cosec x cosec –1 sec x sin –1 cos x cos –1 sin x , then dy/dx is equal to If y = sin (log e x) then x 2 d 2 y/dx 2 xdy/dx is equal to If y = sin1 (5x12√(1x 2))/13, then dy/dx is equal to If y = sin1 (x/2) cos1 (x/2), then the value of dy/dx is If y = sin 2 α cos 2 (αβ) 2 sin α sin βGiven y = a log x Note that derivative for ln x is 1/x (And I think this has been misunderstood by some users here as "derivative for log x is 1/x") From the given function y above, => y = a * (ln x / ln 10) Based on constant multiple rule of de Continue Reading Related Answer Subhasish Debroy , Former SDE at Bharat Sanchar Nigam Limited
We start with the function y = l n ( x) First use exponentiation with the base e to get rid of the log, a common manipulation with log equations, e y = x (*) Now take the derivative of each side, remembering to use the chain rule on ey, because y is a function of x d d x e y = d d x x and If y log 1 cos x 1 cos x 1 2 Show that dy dx cosec x mention each and every formula and minute details Mathematics TopperLearningcom h7b68mm> Starting early can help you score better!Why create a profile on Shaalaacom?
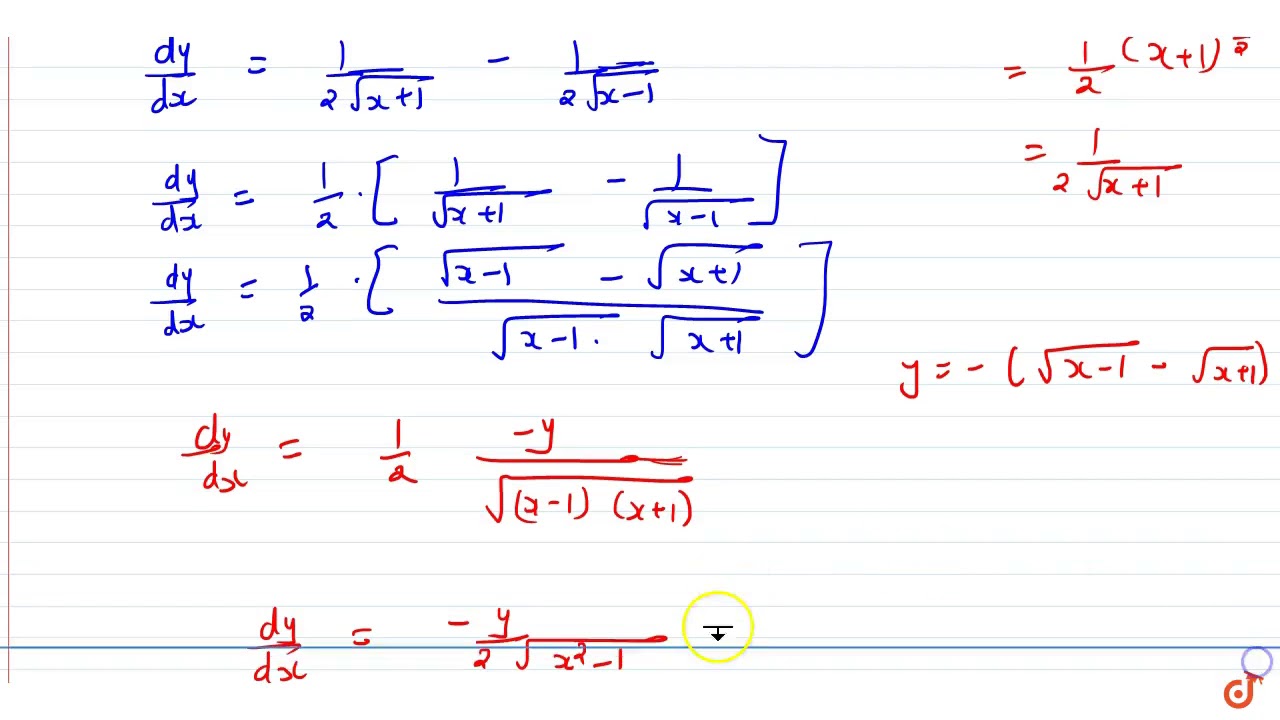



If Y Sqrt X 1 Sqrt X 1 Prove That X 2 1 D 2y Dx 2 X Dy Dx Y 4 0 Youtube




If Log 1 X 2 X Y 1 X
Calculus Find dy/dx y=1/ (x^2) y = 1 x2 y = 1 x 2 Differentiate both sides of the equation d dx (y) = d dx ( 1 x2) d d x ( y) = d d x ( 1 x 2) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more stepsUse logarithmic differentiation to find dy/dx (x 1) (x 2) y = x > 2 (x 1) (x 2)' dy x dx = Find f' (x) and f' (c) Function f (x) = (x5 5x) (2x4 5x – 3) Value of a = C= 0 f' (x) = = x f' (c) = = x Find an equation of the tangent line to the graph at the given point (x 2)2 (y 3)2 = 37, (1, 3) y = x Circle GD 6 2 197 2 0Question If log(x 2y 2)=2tan −1( xy ) then dxdy = A x−yxy B xyx−y C xy1 D None of these Easy Solution Verified by Toppr Correct option is A) Differentiating both sides of the given relation with respect to x, we get, dxd log(x 2y 2)=2 dxd tan −1( xy ) x 2y 21 × dxd (x 2y 2)=2× 1(y/x) 21 × dxd ( xy ) x 2y 21 dxd (x 2) dxd



1




Solved Use Logarithmic Differentiation To Find Dy Dx Y Chegg Com
If y = log((1 x^2)/(1 x^2)), then dy/dx = A 4x^3/1 x^4 B 1/4 x^4 C 1/4 x^4 D 4x^3/1 x^4 ← Prev Question Next Question The correct question is If then prove that Given the equation We have to prove that Given the equation Differentiating with respect to 'x' , we get Multiplying the above equation by , we get Now, Differentiating again with respect to 'x' that is the second order differential of the given function, we get Multiplying the above equation by we get,1 Inform you about time table of exam 2 Inform you about new question papers 3 New video tutorials information




If Xy Log X Y 1 Prove That Dydx Y X 2y X Y X Xy 2 X Y




Solved Find Dy Dx X 2 Xy Y 2 1 X Tan Y Y X X Chegg Com
Y = e x log x Use product rule dy/dx = e x log x e x (1/x) = e x (log x 1/x) Hence option (2) is the answer Was this answer helpful?Find d2y/dx2 where y=log(x^2/e^2) y=log(x 2 /e 2 ) diff wr to x , we get dy/dx=1/(x 2 /e 2 ) (2x/e 2 ) =2/x diff wr to x again d 2 y/dx 2 =2/x 2 ThankDy = y 2 cosx y2 cot x dx (1 –log y ) sin x 1 – log y Answer 3 y cot x 1logy 8 If xy = e x –y, then dy/ dxis equal to 1 y 2 x (1 log x)2 (1 logx)2 3 log x 4 none of these ( 1 logx)2 8 Solution Given that xy = e x –y y log x = (x –y) log ee y
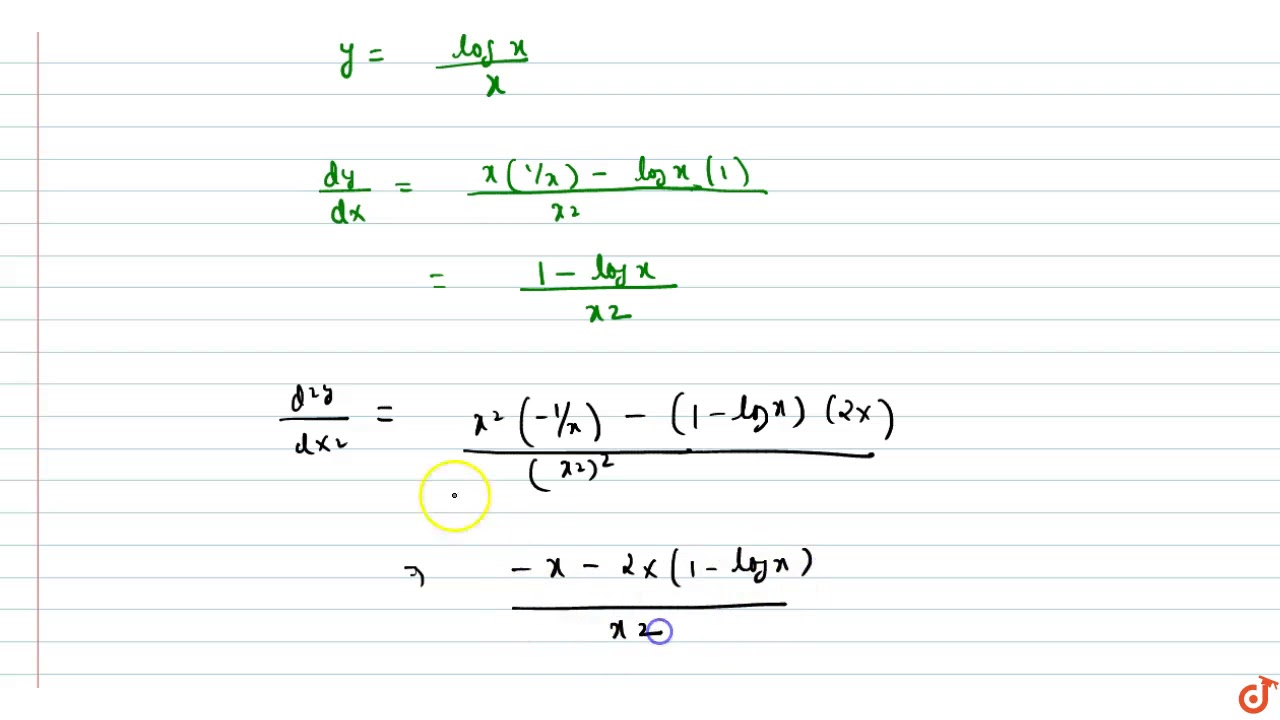



If Y Logx X Show That D 2y Dx 2 X 1 3 Youtube




If Y Log 10 X Then Dy Dx Youtube
Best Answer This is the best answer based on feedback and ratings y= (x1) (x2)/ (x1) (x2) apply logarithms we get if y= log(xroot x21)2 show that (1x2) d2y/dx2 xdy/dx =2 Maths Continuity and DifferentiabilityIf y=logex((x1/x2))1/2, then (dy/dx) equal to (A) 7 (B) (3/x2) (3/(x1)) (D) None of these Check Answer and Solution for above question from




If Y Log 1 X 2 1 X 2 Then Dy Dx Is Equal To




If Y Log 1 2t 2 T 4 X Tan 1 T Find Y Teachoo
Last edited by a moderator ReplyAvail 25% off on study pack Avail Offer Explanation The derivative of y = log(u) is dy dx = loge ⋅ 1 u × d dx (u), since lnx = 1 logelogx, and d(lnx) dx = 1 x Following these exact steps we get dy dx = loge ⋅ 1 x2 1 × 2x The final answer is dy dx = 2xloge x2 1 Answer link



1



If Y Log 1 X 2 1 X 2 Then Dy Dx A 4x 3 1 X 4 B 1 4 X 4 C 1 4 X 4 D 4x 3 1 X 4 Sarthaks Econnect Largest Online Education Community
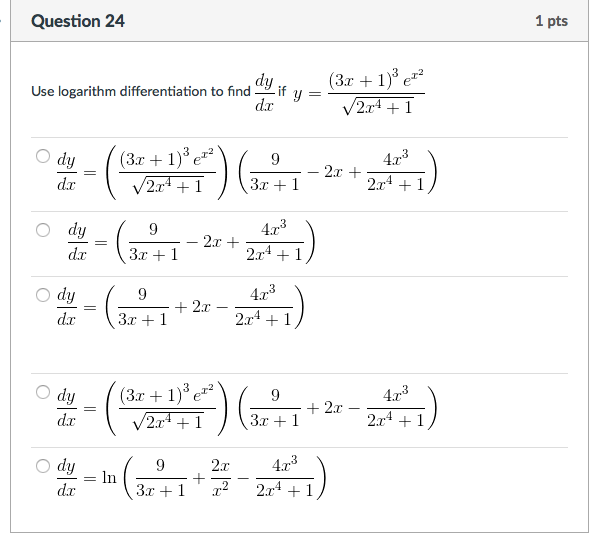
Explanation Here we have to use implicit differentiation As log(xy) = x2 y2 or logx logy = x2 y2 assuming base is e, we have on differentiation 1 x 1 y dy dx = 2x 2y dy dx or dy dx (2y − 1 y) = 1 x −2x or dy dx = 1 x −2x 2y − 1 y = y − 2x2y 2xy2 −x In case base is 10, we can write it as lnx ln10 lny ln10 = x2 y2Find stepbystep solutions and your answer to the following textbook question Use logarithmic differentiation to find dy/dx y = x^(x1)Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep




If Y Log X Root X2 1 Then Prove That X2 1 Dy Dx X Dy Dx 0 Brainly In




3 If Y Log X 1 1 2 X 1 1 2 Then Dy Dx Is A 1 2 X2 1 1 2 B 1 2 X2 1 1 2 C Brainly In
NCERT Solutions, Sample Papers, Notes, Videos Install Now dy/dx=x (2logx1)/sinyycosy Report Posted by Meenakshi Rajput 4 years, 9 months ago CBSE > Class 12 > Mathematics 1 answers Sahdev Sharma 4 years, 9 months ago d y d x = x ( 2 l o g x 1) s i n y y c o s yGiven xyx 2sin , find dxdy by using implicit differentiation Then the correct answer is Then the correct answer is 15 The equations of the tangent line and normal line to the curve xyx 2sin at the point ,0 are given by (1) xy 3 and xy 3 (2) xy 3 and xy 3 Example 9 Find the general solution of the differential equation 𝑑𝑦/𝑑𝑥=(𝑥1)/(2−𝑦) , (𝑦≠2) 𝑑𝑦/𝑑𝑥=(𝑥 1)/(2 − 𝑦) , (𝑦≠2) (2 − y) dy = (x 1) dx Integrating both sides ∫1 〖(2−𝑦)𝑑𝑦=〗 ∫1 (𝑥1)𝑑𝑥 2y − 𝑦^2/2 = 𝑥^2/2 x c 〖4𝑦 − 𝑦〗^2/2 = (𝑥^2 2𝑥 2𝑐)/2 4y − y2 = x2 2x 2c Accounts Tax GST




Find The Derivatives W R T X Y 1 X 1 2x 1 3x 2 Youtube



If Y Log X 1 X 2 Then Prove That X X 1 2y2 X 1 2y1 2 Sarthaks Econnect Largest Online Education Community
4 (29) (68) (25) Choose An Option That Best Describes Your Problem Answer not in Detail Incomplete Answer Answer Incorrect Others Answer not in Detail Incomplete AnswerLHS log(y) => (1/y)(dy/dx) partial differentiation hence we multiply (1/y) by dy/dx RHS x log(2) => log(2) log(2) is a constant so x dissapears So we get (1/y)(dy/dx) = log(2) 4) We want to find dy/dx, which is on the LHS To get this dy/dx on its own we can multiply both sides by y So we get dy/dx = y log(2) 5) To finish this Ex 94, 12 Find a particular solution satisfying the given condition 𝑥 𝑥2−1 𝑑𝑦𝑑𝑥=1;𝑦=0 When 𝑥=2 𝑥 𝑥2−1 dy = dx dy = 𝑑𝑥𝑥(𝑥2 − 1) Integrating both sides 𝑑𝑦 = 𝑑𝑥𝑥(𝑥2 − 1) 𝑦 = 𝑑𝑥𝑥(𝑥 1)(𝑥 − 1) We can write integrand as 1𝑥(𝑥 1
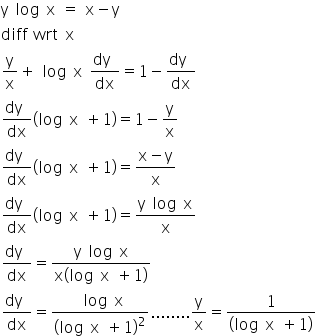



If Y Log X X Y Prove That Dy Dx Log X 1 Log X 2 Mathematics Topperlearning Com 2dolmeyy




Form Differential Equation 1 Y 2 1 Log X Dx Xdy 0 Given Y 1 When X 1
Get Answer to any question, just click a photo and upload the photo and get the answer completely free, UPLOAD PHOTO AND GET THE ANSWER NOW!Solution Verified by Toppr Correct option is A) We have, y=log( 1x 21−x 2 ) ⇒y=ln(1−x 2)−ln(1x 2), using log ba =loga−logb Now differentiate ⇒ dxdy = 1−x 2−2x − 1x 22x =−2x( 1−x 21 1x 21 ) =−2x( (1−x 2)(1x 2)1x 21−x 2 )= 1−x 4−4x Video Explanation Solve any question of Continuity and Differentiability with Patterns of problems >First dy/dx = (y/x 1)/ (y/x 1) Taking y = vx dy/dx = v xdv/dx Therefore, dx/x = (v 1)dv / (v^2 1) Integrating we get log (1/x) logc = arctan (y/x) 1/2 log How to show that dxdy = d(x−c)dy ?




If Y Log Root X 1 Root 2 Then Prove X X 1 2 Y2 X 1 2 Y1




If Y Log 1 X 2 1 X 2 Then Find Dy Dx Maths Meritnation Com
Y = log(log(logx)) 2 Differentiating both sides wrt x, we get `"dy"/"dx" = "d"/"dx" log(log(log "x"))^2` `= 2log(log(log "x")) xx "d"/"dx" log(log(log "x"))`Check here stepbystep solution of 'If log(√1x^2−x) = y√1x^2 find (1x^2) dy/dx xy 1 = 0' question at Instasolv! Solve dy/dx = (y^2 1)/ (x^2 1), y (2) = 2 Relevant Equations dy/dx = (y^2 1)/ (x^2 1), y (2) = 2 This is my attempt Since y (2) = 2, So, Is this ok, or did I make any mistake?



If Y X 2 1 Log X X 2 1 Prove That X 2 1 Dy Dx Xy 1 Quora




Solved Find Dy Dx Given That Y Ln Squareroot X 2 1 Ln X Chegg Com
Find dy/dx y = natural log of x^2 y = ln (x2) y = ln ( x 2) Differentiate both sides of the equation d dx (y) = d dx (ln(x2)) d d x ( y) = d d x ( ln ( x 2)) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps Differentiate using the chain rule, which states thatWorkdone =(1/2)kx^2 given, stretching the string from 4 to 12Find in terms of x and y x°y° = 3 Q Compute the work required to stretch a spring from 4 to 12 cm past equilibrium, assuming that the A the equation to find workdone is;




Solved Assignment 1 If Y Xsinx Find Dx Dy 2 If Y Chegg Com




If Y Log X Sqrt X 2 A 2 Show That X 2 A 2 D 2y Dx 2 X Dy Dx 0 Youtube
Answer (1 of 5) Sorry, but I didn't had time to type those \displaystyle \LaTeX , so wrote on paper and snapped its picture p > The solution could be very short If y = (1 1/x2)/(1 1/x2), then dy/dx is Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to Textbook solution Answer from CBSE Board Exam Mathematics Read on Answer 50 /5 5 Brainly User Answer y = logx^ x y = x log x ( bcz log m^ n = n log m) then , dy / dx = x { d / dx ( log x) } log x { d / dx ( x) } dy / dx = x ( 1 / x) log x ( 1) _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ " dy / dx = 1 log x Ans Hope it will Help you ️



If Y Log X 2 X 1 X 2 X 1 2 3 Tan 1 3x 1 X 2 Find Dy Dx Sarthaks Econnect Largest Online Education Community




If Y Log X Sqrt 1 X 2 Prove That Sqrt 1 X 2 Dy Dx 1 Youtube
Ie f (x)g (x)=f (x) d/dx g (x) g (x) d/dx f (x) dy/dx= (1log (x1)) (1log (x1)) dy/dx=log (x1)log (x1) Now using property {log a pq=log a plog a q} Final answer=log (x1/x1)=RHS Think You Can Provide A Better Answer ?Find stepbystep solutions and your answer to the following textbook question Use logarithmic differentiation to find dy/dx y= (x1)(x2) / (x1)(x2), x > 2Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



1
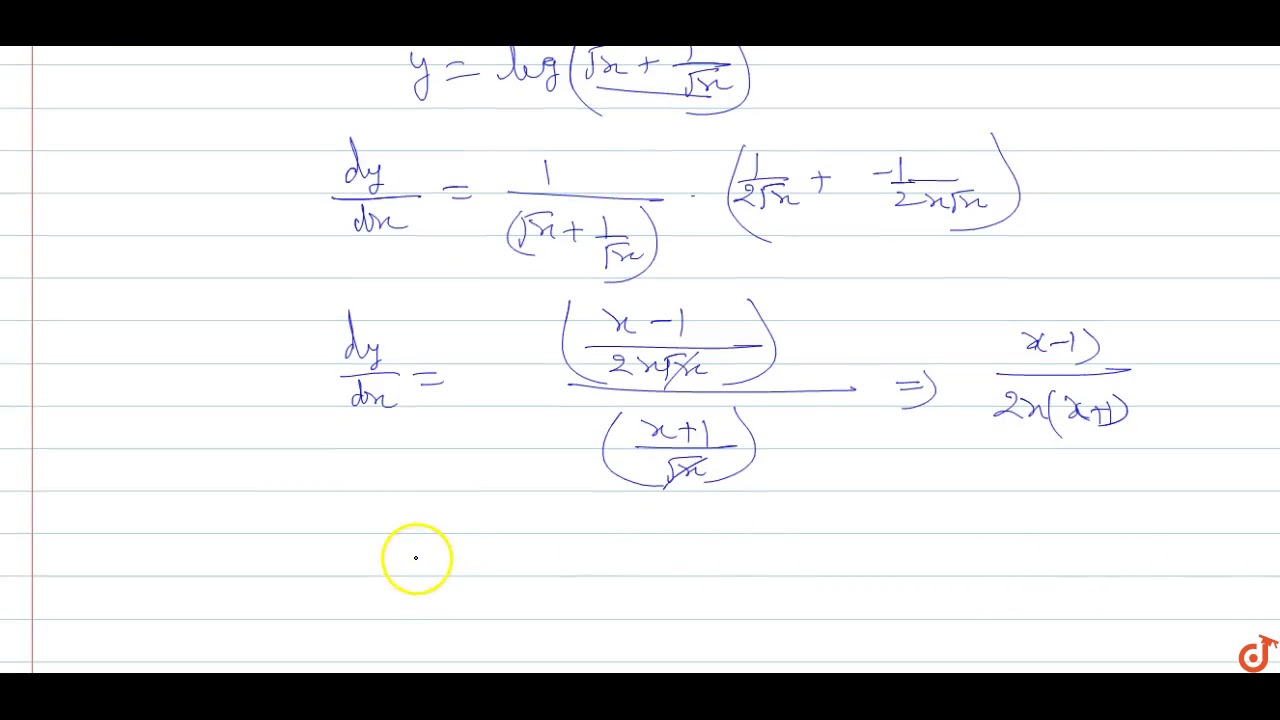



If Y Log Sqrt X 1 Sqrt X Prove That Dy Dx X 1 2x X 1 Youtube
The derivative of the function with respect to x, has to be determined It is assumed that log in the problem refers to natural logarithm Use the chain rule here Let and y = log z andSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreGet Answer to any question, just click a photo and upload the photo and get the answer completely free, UPLOAD PHOTO AND GET THE ANSWER NOW!



Differentiate The Following Functions With Respect To X Log X 2 X 2 4x 1 Sarthaks Econnect Largest Online Education Community



1




If Y Log X X 2 A 2 X 2 A 2 X Find Dy Dx Target Batch




If Y Log 1 Sin 2x 1 Tanx Find Dy Dx Maths Continuity And Differentiability Meritnation Com
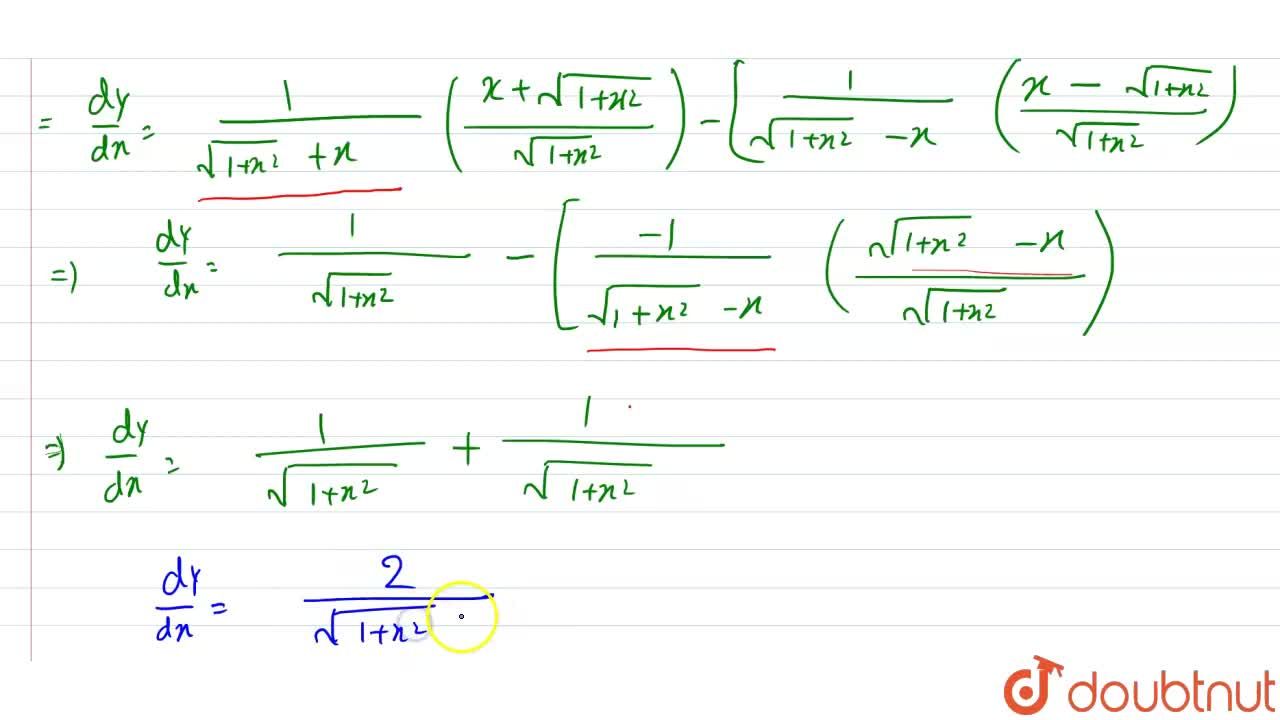



If Y Log Sqrt 1 X 2 X Sqrt 1 X 2 X Then Dy Dx




If Y Log X 1 X2 1 2 Prove That Dy Dx 1 Log X 1 X2 1 2 1 1 X2 1 2 Mathematics Topperlearning Com Qsw6n0xx




If Y Log Sin X 2 1 Prove That Dy Dx Xcot X 2 X 1 Brainly In




Hi My Question Is If Y Log X 1 X 2 1 2 2 Find Dy Dx And D 2y Dx 2 Maths Continuity And Differentiability Meritnation Com



If Y Log X X 1 How Do You Prove That X 1 D Y Dx X D Y Dx 0 Quora




If Y Log E Tan 1 1 X 2 Find Dy Dx



If Y X 2 1 Log 1 X 1 1 X 2 Find Dy Dx Sarthaks Econnect Largest Online Education Community



How To Solve This Problem 1 X 2 D 2y Dx 2 1 X Dy Dx Y Sin 2log 1 X Quora



5 Derivative Of The Logarithmic Function




If Y Log 1 Cos2 X 1 E2x 1 2 Show That Dy Dx E2x 1 E2x Sin X Cos X 1 Cos2 X Show Each And Every Step Mathematics Topperlearning Com Idjkxezz



Solved Use Logarithm Differentiation To Find If Dy Dx If Y Chegg Com
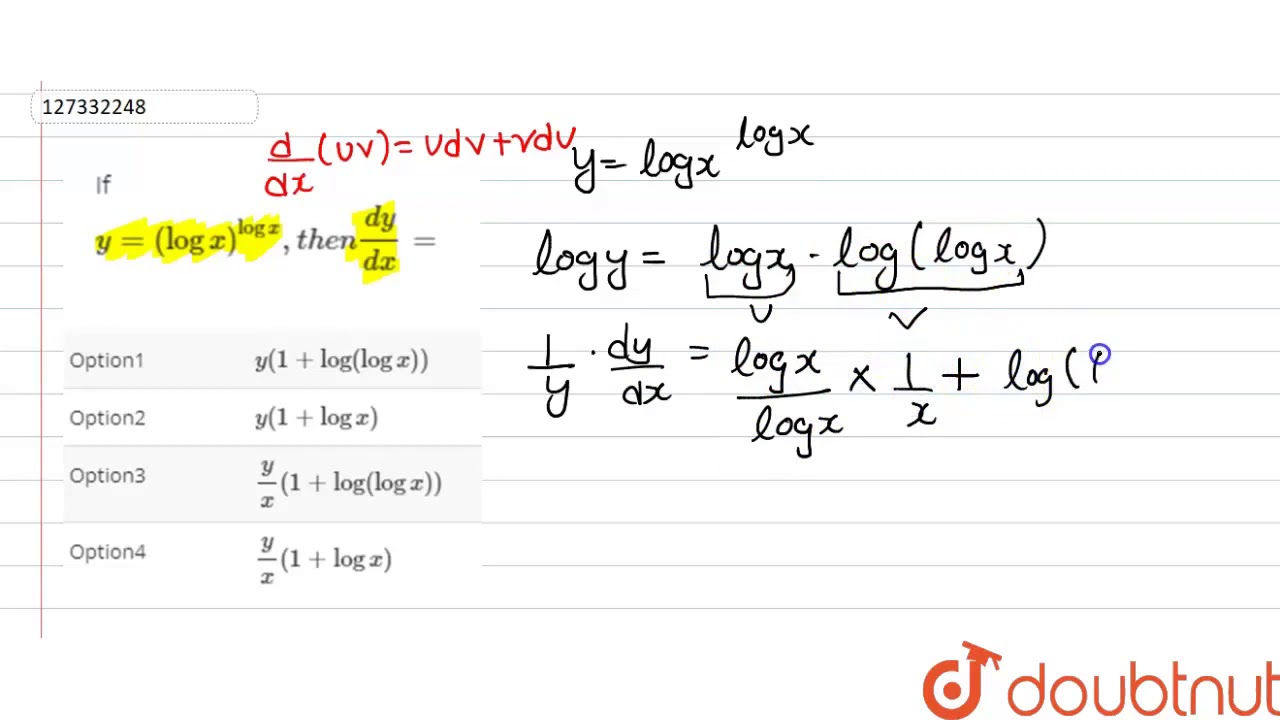



If Y Log X Logx Then Dy Dx Youtube




If Y Log 1 X 1 X 1 4 1 2tan 1 X T H E N Dy Dx
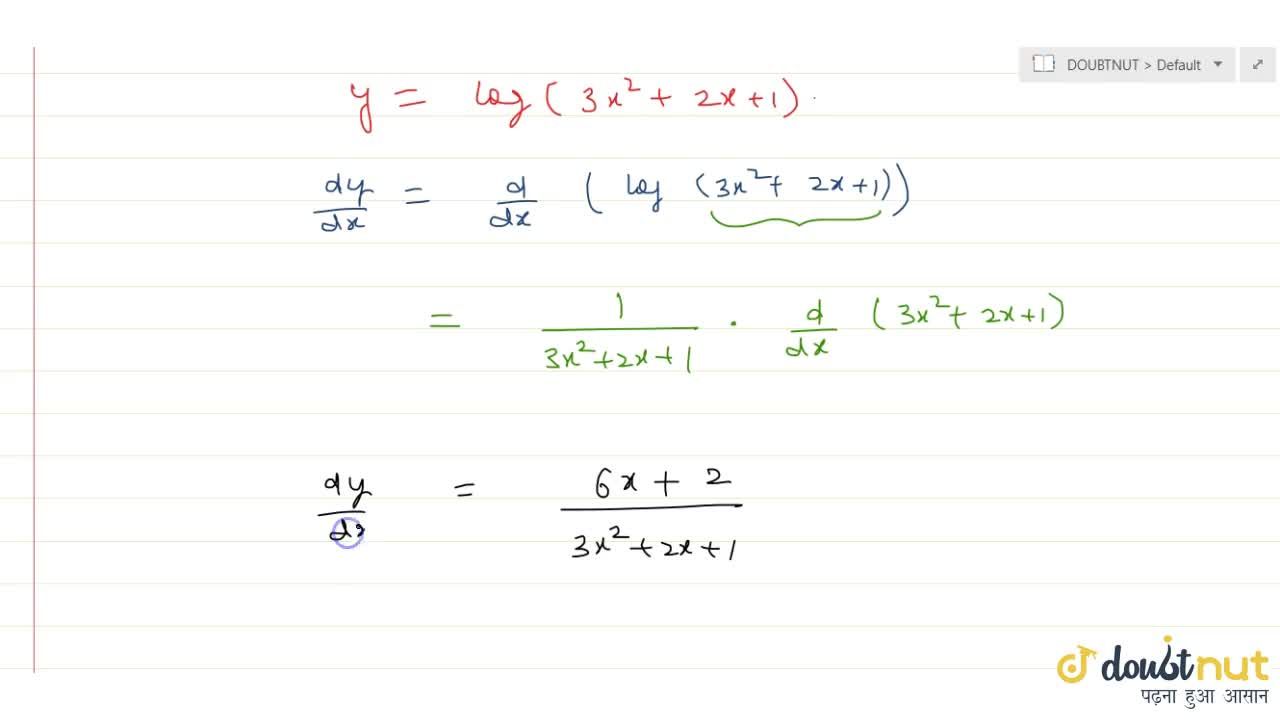



Y Log 3x 2 2x 1 F I N D Dy Dx




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X



If Y X 2 1 Log 1 X 1 1 X 2 Find Dy Dx Sarthaks Econnect Largest Online Education Community




Y Log X Root 1 X2 Prove That 1 X2 D2y Dx2 X Dy Dx 0 Brainly In




Solved Dy 3 Find Dx A Y 24 Log X2 1 C Y In X In X Chegg Com




3 X 1 4 X 1 29 4x 1




Find Dy Dx Of X 2 Cosx X 2 1 X




Solved Use Logarithmic Differentiation To Find Dy Dx Y Chegg Com




If Log X 2 Y 2 Tan 1 Yx Then Prove That Dydx X Yx Y



How To Get The Special Solution Of This Differential Equation Y Xdy Dx 2 1 X 2 Dy Dx Where X 1 Y 1 Quora




If Y Log X X Y Then Prove Dy Dx Log X 1 Log X 2 Brainly In




Ex 6 2 7 Show That Y Log 1 X 2x 2 X Is An Increasing Fn



How To Find Dy Dx Of The Function Y X 1 X 2 X 1 2 Quora




Mathematics Statistics 1 Pages 101 150 Flip Pdf Download Fliphtml5



If Y Log 1 X 2 1 X 2 Then Dy Dx A 4x 3 1 X 4 B 1 4 X 4 C 1 4 X 4 D 4x 3 1 X 4 Sarthaks Econnect Largest Online Education Community




Solved Derivatives Of Logarithmic Functions Find Dy Dx Y Chegg Com




If Y Log X Root X2 1 Then Prove That X2 1 Dy Dx X Dy Maths Meritnation Com




Mathematics Statistics 1 Pages 101 150 Flip Pdf Download Fliphtml5



If Xy E X Y Then Prove That Dy Dx Log X 1 Log X 2 Sarthaks Econnect Largest Online Education Community




Solved Section 3 1 6 9 16 25 Section 3 2 7 11 15 Chegg Com



What Is The Derivative Of Log X 1 X Quora




If Y Log E 3x X 4 X 3 2 3 Then Find Dydx




1 If Y Sqrt X 2 1 Log 1 X Sqrt 1 1 X 2 Find Dy Dx 2 Find The Equation Of Tangent To The Curve Y Sqrt 4x 2 Which




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X




If Y Log 1 Cos 2 X1 E 2x Show That Dydx E 2x 1 E 2x Sinxcosx 1 Cos 2 X




If Y X 2 1 Log 1 X 1 1x 2 Then Find Dy Dx Brainly In




If Y Log 1 X 2 1 X 2 Then Dy Dx A 4x 3 1 X 4 B 4x 1 X 4 C 1 4 X 4 D 4x 3 1 X 4




Solved Find Dy Dx For Y X 3 Squareroot X 1 3x 2 2 Chegg Com




Can Anyone Please Help Me Do This If Log X Aˆs 1 X2 2 Show That 1 X2 D2y Dx2 X Dy Dx 2 0 Maths Differential Equations Meritnation Com




Find Dy Dx Of Sqrt X 1 X 2 X 3 X




Ex 5 5 7 Differentiate The Function Log X X X Log X



What Is The Derivative Of 1 Logx Quora




If Ylog X X Y Prove That Dydx Logx 1 Logx 2




Solved If Y Log X 1 2 X 2 X 1 Find Dy Dx At X 5 B Chegg Com




If Log X Y Log 2 1 2 Log X 1 2 Log




If Y Log Root X 1 Root 2 Then Prove X X 1 2 Y2 X 1 2 Y1




If Y Log X Sqrt X 2 A 2 Show That X 2 A 2 D 2 Y Dx 2 X Dy Dx 0 Youtube



What Is The Second Derivative Of Y Log X 2 E X Quora




If Y X 2 1 Log X 2 1 X Show That X 2 1 Dydx Xy 1 0




If Y Log Sqrt X 1 Sqrt X 1 Then Dy Dx Is Equal To Youtube



How To Solve X 2 D 2 Y Dx 2 Xdy Dx Y Log X Quora



What Is The Derivative Of The Logarithmic Function Y Log 4x 1 4x 1 Quora




If Y Log Sqrt 1 Sinx 1 Sinx Find The Value Of Dy Dx Youtube




Solved Section 3 1 6 9 16 25 Section 3 2 7 11 15 Chegg Com




If Y Log X X Then The Value Of Dy Dx Is Youtube




Y Log Sqrt 1 Cos 3x 2 1 Cos 3x 2 Differentiate W R T X Youtube




Misc 14 Find Particular Solution X 1 Dy Dx 2e Y 1




If Y Log 1 X 21 X 2 Then Dydx Is Equal To
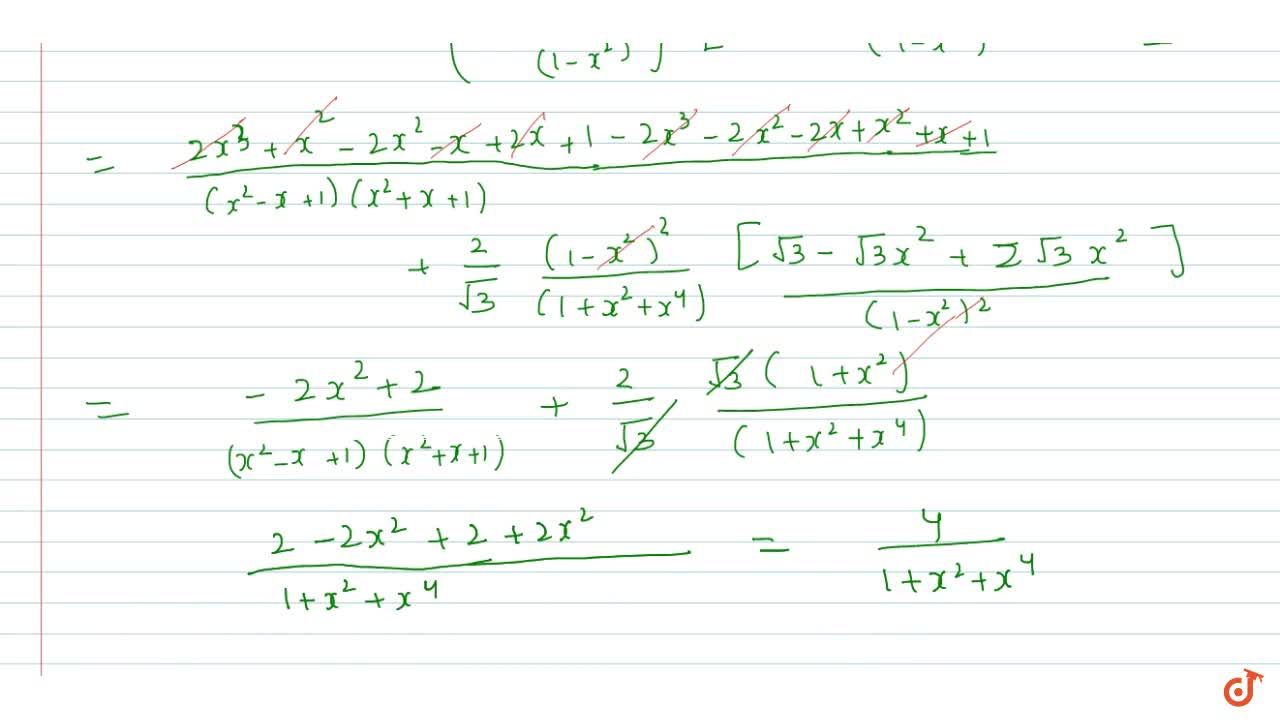



If Y Log X 2 X 1 X 2 X 1 2 Sqrt 3 T A N 1 Sqrt 3 X 1 X 2 F I N D Dy Dx




1 If Y Sqrt X 2 1 Log 1 X Sqrt 1 1 X 2 Find Dy Dx 2 Find The Equation Of Tangent To The Curve Y Sqrt 4x 2 Which



How To Expand Log 1 Log 1 X In Powers Of X As Far As X 4 Quora




Worked Example Implicit Differentiation Video Khan Academy
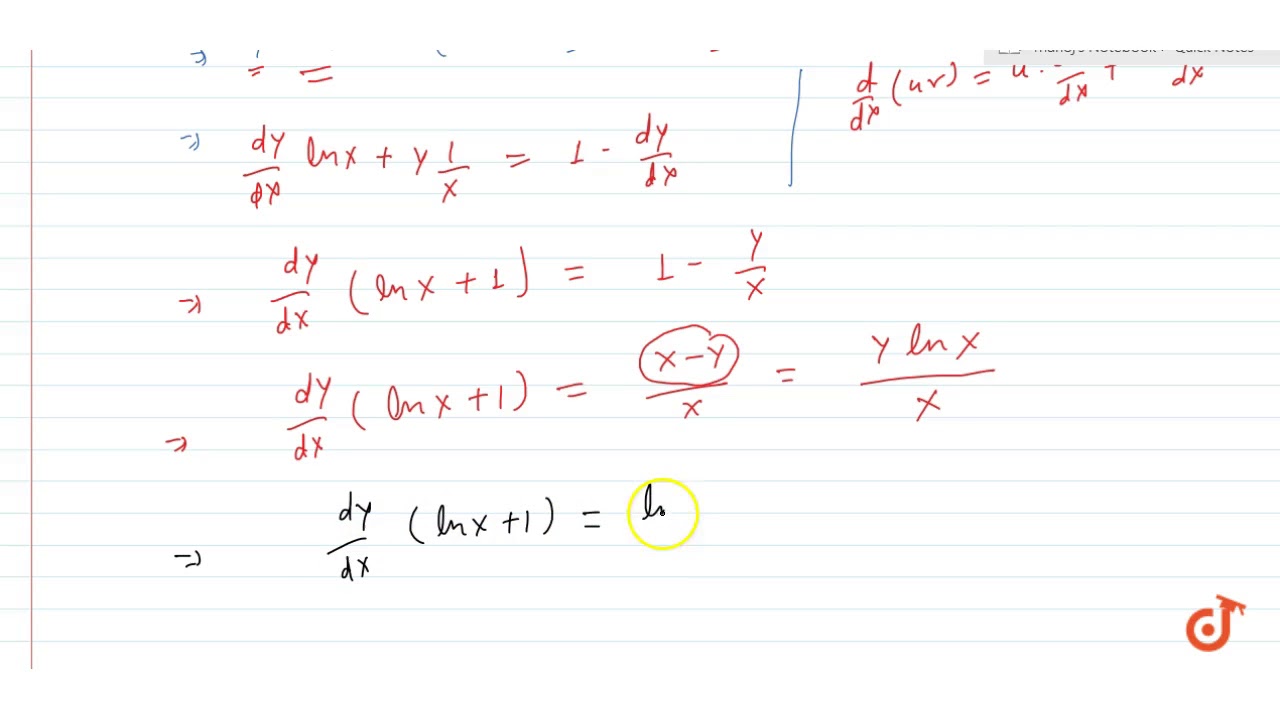



X Y E X Y So Prove That Dy Dx Logx 1 Logx 2 Youtube




If Y Log X Sqrt X 2 1 Prove That X 2 1 D 2 Y Dx 2 X Dy Dx 0 Youtube




If X Sqrt 1 U 2 Y Log 1 U 2 Then Dy Dx
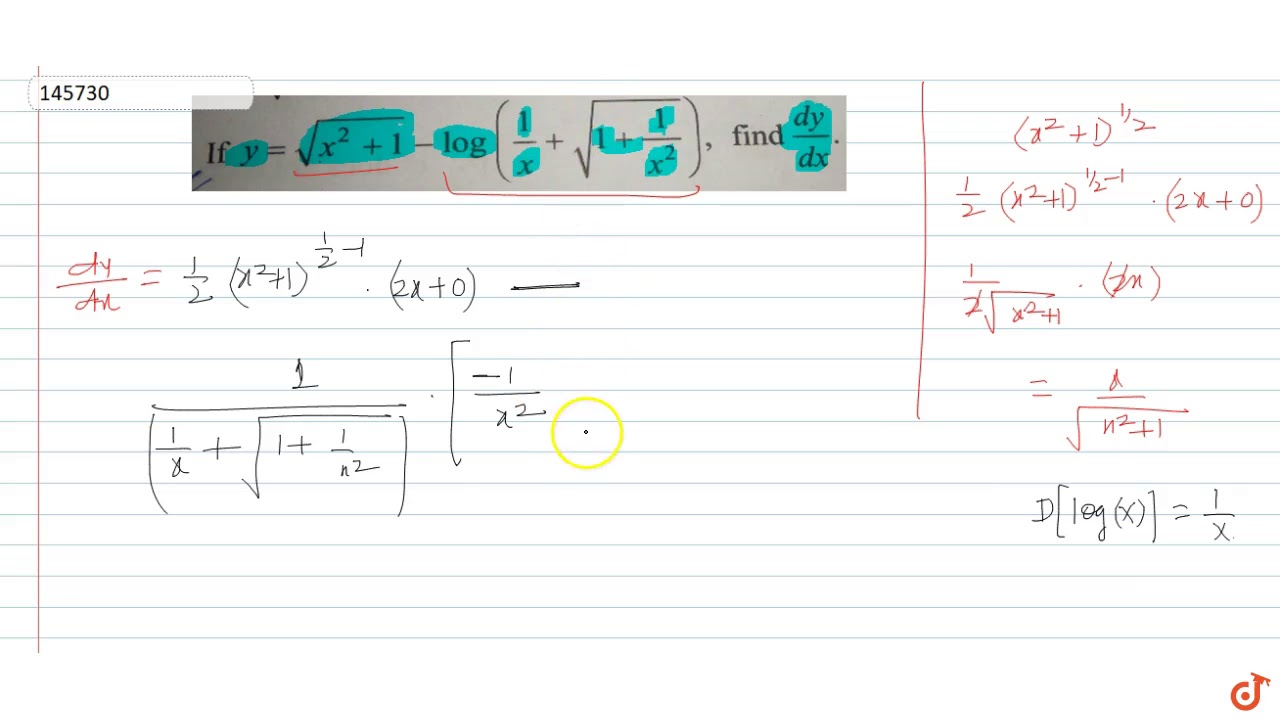



Y Sqrt X 2 1 Log 1 X Sqrt 1 1 X 2 Find Dy Dx Youtube




Engineering Mathematics Notes



How To Find Dy Dx Of The Function Y X 1 X 2 X 1 2 Quora




Derivative Of Log X Sqrt X 2 A 2 W R T X Is Youtube



0 件のコメント:
コメントを投稿